Epicycloid
A planar curve given by the trajectory of a point on a circle rolling on the exterior side of another circle. The parametric equations are:
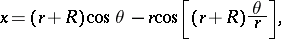 |
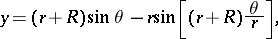 |
where  is the radius of the rolling and
is the radius of the rolling and 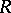 that of the fixed circle, and
that of the fixed circle, and 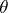 is the angle between the radius vector of the point of contact of the circles (see Fig. a, Fig. b) and the
is the angle between the radius vector of the point of contact of the circles (see Fig. a, Fig. b) and the  -axis.
-axis.
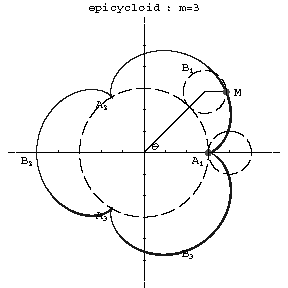
Figure: e035860a
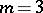

Figure: e035860b
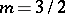
Depending on the value of the modulus 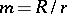 , the resulting epicycloid has different forms. For
, the resulting epicycloid has different forms. For 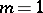 it is a cardioid, and if
it is a cardioid, and if 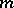 is an integer, the curve consists of
is an integer, the curve consists of 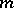 distinct branches. The cusps
distinct branches. The cusps 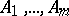 have the polar coordinates
have the polar coordinates 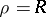 ,
, 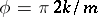 ,
, 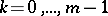 . The vertices
. The vertices 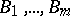 of the curve have the coordinates
of the curve have the coordinates 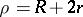 ,
, 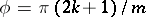 . When
. When 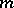 is a rational fraction, the branches intersect each other in the interior; when
is a rational fraction, the branches intersect each other in the interior; when 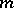 is irrational there are infinitely many branches and the curve does not return to a point
is irrational there are infinitely many branches and the curve does not return to a point 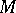 describing a position obtained previously; for rational
describing a position obtained previously; for rational 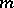 the epicycloid is a closed algebraic curve. The arc length from the point
the epicycloid is a closed algebraic curve. The arc length from the point 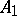 is:
is:
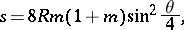 |
and from 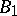 it is
it is
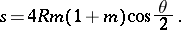 |
The area of a sector bounded by two radius vectors of the curve and its arc is
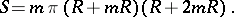 |
The radius of curvature is
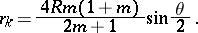 |
When the point is not situated on the rolling circle, but lies in its exterior (or interior) region, then the curve is called an elongated (respectively, shortened) epicycloid or epitrochoid (see Trochoid). Epicycloids belong to the so-called cycloidal curves (cf. Cycloidal curve).
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
Epicycloids (and hypocycloids, cf. Hypocycloid) have many equivalent definitions. See, e.g., [a3], pp. 273-277. Epicycloids and, more generally, trochoids are important for kinematical constructions, cf. [a1].
References
| [a1] | H.-R. Müller, "Kinematik" , de Gruyter (1963) |
| [a2] | K. Strubecker, "Differential geometry" , I , de Gruyter (1964) |
| [a3] | M. Berger, "Geometry" , I , Springer (1977) |
| [a4] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
Epicycloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epicycloid&oldid=32757