Lemniscates

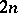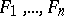Plane algebraic curves of order such that the product of the distances of each point of the curve from given points (foci) is equal to the -th power of a given number (the radius of the lemniscate). The equation of a lemniscate in rectangular Cartesian coordinates is

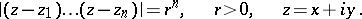A circle is a lemniscate with one focus, and a Cassini oval is a lemniscate with two foci. See also Bernoulli lemniscate and Booth lemniscate.

References

[a1]	F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971)

A lemniscate is a level curve of a polynomial. If all the foci 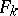: 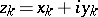, , 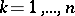are distinct and the radius of the lemniscate is sufficiently small, then the lemniscate consists of continua that have pairwise no common points. For a sufficiently large radius a lemniscate consists of one connected component. As D. Hilbert showed in 1897, the boundary 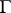of an arbitrary simply-connected finite domain can be arbitrarily closely approximated by a lemniscate, that is, for any 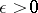one can find a lemniscate 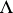such that in the -neighbourhood of each point of 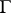there are points of 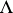and every point of 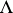is in the -neighbourhood of an appropriate point of .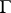

References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian)
[2]	J.L. Walsh, "Interpolation and approximation by rational functions in the complex domain" , Amer. Math. Soc. (1965)

E.D. Solomentsev