Parallel surfaces
Diffeomorphic equi-oriented surfaces  and
and  having parallel tangent planes at corresponding points and such that the distance
having parallel tangent planes at corresponding points and such that the distance  between corresponding points of
between corresponding points of  and
and  is constant and equal to that between the corresponding tangent planes. The position vectors
is constant and equal to that between the corresponding tangent planes. The position vectors  and
and  of two parallel surfaces
of two parallel surfaces  and
and  are connected by a relation
are connected by a relation 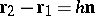 , where
, where 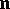 is a unit normal vector that is the same for
is a unit normal vector that is the same for 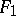 at
at 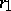 and
and 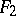 at
at 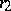 .
.
Thus, one can define a one-parameter family  of surfaces parallel to a given
of surfaces parallel to a given 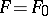 , where
, where  is regular for sufficiently small values of
is regular for sufficiently small values of  for which
for which
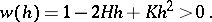 |
To the values of the roots  and
and  of the equation
of the equation 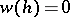 there correspond two surfaces
there correspond two surfaces 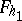 and
and 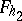 that are evolutes of
that are evolutes of 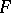 , so that parallel surfaces have a common evolute (cf. Evolute (surface)). The mean curvature
, so that parallel surfaces have a common evolute (cf. Evolute (surface)). The mean curvature 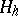 and the Gaussian curvature
and the Gaussian curvature 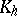 of a surface
of a surface 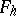 parallel to
parallel to 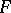 are connected with the corresponding quantities
are connected with the corresponding quantities 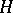 and
and 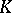 of
of 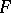 by the relations
by the relations
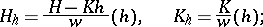 |
lines of curvature of parallel surfaces correspond to each other, so that between them there is a Combescour correspondence, which is a special case of a Peterson correspondence.
Comments
For a linear family of closed convex parallel surfaces (depending linearly on a parameter  ) the Steiner formula holds: The volume of the point set bounded by them is a polynomial of degree 3 in
) the Steiner formula holds: The volume of the point set bounded by them is a polynomial of degree 3 in  . An analogous result holds for arbitrary dimensions. The Steiner formula is a special case of formulas for general polynomials in Minkowski's theory of mixed volumes, and, even more general, in the theory of valuations.
. An analogous result holds for arbitrary dimensions. The Steiner formula is a special case of formulas for general polynomials in Minkowski's theory of mixed volumes, and, even more general, in the theory of valuations.
For references see Parallel lines.
Parallel surfaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallel_surfaces&oldid=32709