Transcendency, measure of
transcendence measure
A function characterizing the deviation of a given transcendental number from a set of algebraic numbers of bounded degree and bounded height under a change of bounds on these parameters. For a transcendental number 
and natural numbers 
and 
, the measure of transcendency is
 |
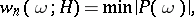where the minimum is taken over all non-zero integer polynomials of degree not exceeding 
and height not exceeding 
. It follows from Dirichlet's "box" principle (cf. Dirichlet principle) that the following always holds:
 |
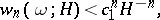where 
depends only on 
. In many cases it is possible to obtain not only a proof of the transcendency of a number 
but also a lower bound for the measure of transcendency in terms of the degree, and logarithmic or exponential functions of 
and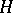 
. For example, Hermite's method of proof of transcendency of 
enables one to obtain the inequality
 |
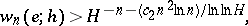where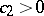 
is an absolute constant and 
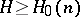. For any fixed 
and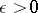 
,
 |
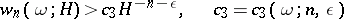for almost-all (in the sense of Lebesgue) real numbers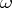 
(see Mahler problem). Transcendental numbers can be classified on the basis of the difference in asymptotic behaviour of 
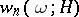under unrestricted variation of 
and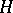 
(see [3]).
References
| [1] | A.O. Gel'fond, "Transcendental and algebraic numbers" , Dover, reprint (1960) (Translated from Russian) |
| [2] | P.L. Cijsouw, "Transcendence measures" , Univ. Amsterdam (1972) (Dissertation) |
| [3] | A. Baker, "Transcendental number theory" , Cambridge Univ. Press (1975) |
Comments
References
| [a1] | A.B. Shidlovskii, "Transcendental numbers" , de Gruyter (1989) (Translated from Russian) |
Transcendency, measure of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendency,_measure_of&oldid=32681