Fano scheme

of a projective algebraic variety 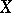over a field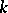

The algebraic scheme parametrized by the family of lines lying on the subvariety 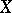of the projective space 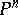. The Fano scheme 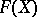of a projective variety 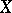can be given as a closed subscheme of the Grassmannian 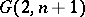of lines in 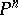. In contrast to the Fano scheme of a three-dimensional cubic (see Fano surface), the Fano scheme of an arbitrary projective variety does not have to be non-singular, reduced or irreducible. Thus, the ruled surface 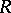of lines lying on the Fermat cubic 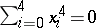consists of 40 cones cut out by the hyperplanes 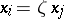, , 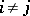where 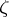ranges over the primitive 8th roots of unity. Each of the cones enters in 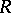with multiplicity 2 (see [1]). Thus, this Fano variety is reducible and each component of it is not reduced at a generic point.

References

[1]	B. Tennison, "On the quartic threefold" Proc. London Math. Soc. , 29 (1974) pp. 714–734