Pure subgroup

serving subgroup

A subgroup 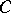of an Abelian group 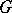such that for any the solvability of the equation in 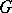implies its solvability in 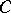. Examples of pure subgroups are the zero subgroup, 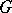itself, the torsion part of 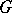, and direct summands. Not every pure subgroup need be a direct summand, even for a 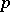-group. However, if 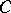is a torsion pure subgroup of an Abelian group and if the orders of its elements are uniformly bounded, then is a direct summand in 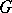. There is a complete description of the Abelian groups in which every pure subgroup is a direct summand (see [1]). The question of the cardinality of the set of pure subgroups of an Abelian group has been thoroughly investigated.

References

[1]	A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian)

References

[a1]	D.J.S. Robinson, "A course in the theory of groups" , Springer (1982)