Normal space (to a surface)
From Encyclopedia of Mathematics
at a point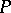 
The orthogonal complement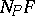 
to the tangent space 
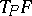(see Tangent plane) of the surface 
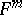in 
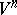at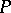 
. The dimension of the normal space is 
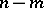(the codimension of 
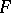). Every one-dimensional subspace of it is called a normal to 
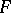at 
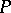. If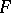 
is a smooth hypersurface, then it has a unique normal at every of its points.
Comments
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
| [a2] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
How to Cite This Entry:
Normal space (to a surface). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_space_(to_a_surface)&oldid=32594
Normal space (to a surface). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_space_(to_a_surface)&oldid=32594
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article