Defining system of neighbourhoods
From Encyclopedia of Mathematics
of a set 
in a topological space 
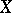
Any family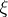 
of subsets of the space 
subject to the following two conditions: a) for every 
there is an open set 
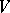in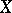 
such that 
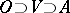; b) for any open set 
in 
containing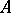 
there is an element 
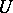of the family 
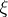contained in 
.
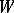It is sometimes further supposed that all elements of the family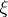 
are open sets. A defining system of neighbourhoods of a one-point set 
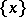in a topological space 
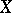is called a defining system of neighbourhoods of the point 
in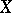 
.
References
| [1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
Comments
A defining system of neighbourhoods is also called a local base or a neighbourhood base.
How to Cite This Entry:
Defining system of neighbourhoods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Defining_system_of_neighbourhoods&oldid=32509
Defining system of neighbourhoods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Defining_system_of_neighbourhoods&oldid=32509
This article was adapted from an original article by A.V. Arkhangel'skii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article