Invertible element

of a semi-group with identity

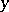An element for which there exists an element such that 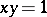(right invertibility) or 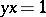(left invertibility). If an element is invertible on both the right and the left, it is called two-sidedly invertible (often simply invertible). The set 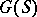of all elements with a two-sided inverse in a semi-group 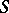with identity is the largest subgroup in 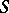that contains the identity. A bicyclic semi-group provides an example of the existence of elements that are invertible only on the right or only on the left; in addition, the existence of such elements in a semi-group 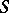implies the existence in 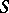of a bicyclic sub-semi-group with the same identity as 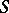. An alternative situation is that in which every element in 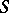with a one-sided inverse has a two-sided inverse; this holds if and only if either 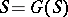or if 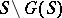is a sub-semi-group (being, clearly, the largest ideal in 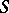); such a semi-group is called a semi-group with isolated group part. The following are examples of semi-groups with isolated group part: every finite semi-group with identity, every commutative semi-group with identity, every semi-group with two-sided cancellation and identity, and every multiplicative semi-group of complex matrices containing the identity matrix.

References

[1]	A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1 , Amer. Math. Soc. (1961)
[2]	E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian)