Weierstrass criterion
From Encyclopedia of Mathematics
for a minimal surface
For a two-dimensional surface in 
-dimensional Euclidean space 
, 
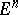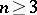, with isothermal coordinates 
and 
of class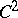 
, to be minimal (cf. Minimal surface), it is necessary and sufficient that the components of its position vector be harmonic functions of 
.
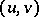Comments
References
| [a1] | J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975) pp. §455 |
| [a2] | K. Weierstrass, "Math. Werke" , 3 , G. Olms, reprint (1967) |
How to Cite This Entry:
Weierstrass criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_criterion&oldid=32376
Weierstrass criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_criterion&oldid=32376
This article was adapted from an original article by I.Kh. Sabitov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article