Hessian (algebraic curve)
From Encyclopedia of Mathematics
of an algebraic curve of degree 
The set of points whose conic polars can be split into two straight lines, as well as the set of double points of the first polars. The Hessian of a non-singular curve of degree  is a curve of degree
is a curve of degree 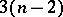 and class
and class 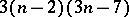 . If
. If 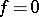 is the equation of a curve of degree
is the equation of a curve of degree  in homogeneous coordinates and if
in homogeneous coordinates and if  , then
, then
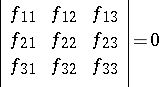 |
is the equation of the Hessian. The Hessian of a non-singular curve of degree 3 in characteristic not equal to three intersects the curve at nine ordinary points of inflection. Named after O. Hesse (1844).
Comments
References
| [a1] | J.L. Coolidge, "A treatise on algebraic plane curves" , Dover, reprint (1959) |
How to Cite This Entry:
Hessian (algebraic curve). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hessian_(algebraic_curve)&oldid=32348
Hessian (algebraic curve). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hessian_(algebraic_curve)&oldid=32348
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article