Normal sub-semi-group
From Encyclopedia of Mathematics
of a semi-group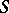 
A sub-semi-group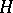 
satisfying the following condition: For any 
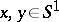(for the notation 
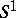see Normal complex) such that 
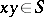and for any 
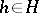the relations 
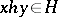and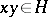 
are equivalent. A subset of 
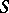is a normal sub-semi-group if and only if it is the complete inverse image of the unit element under some homomorphism of 
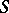onto a semi-group with unit element.
References
| [1] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
How to Cite This Entry:
Normal sub-semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_sub-semi-group&oldid=32024
Normal sub-semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_sub-semi-group&oldid=32024
This article was adapted from an original article by L.N. Shevrin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article