Chasles theorem
If 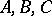 are three arbitrary points on a straight line, then
are three arbitrary points on a straight line, then  , where
, where 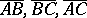 are the lengths of the directed line segments. Chasles' theorem can be generalized to the case of the surface of oriented triangles and the volumes of oriented tetrahedra (see ).
are the lengths of the directed line segments. Chasles' theorem can be generalized to the case of the surface of oriented triangles and the volumes of oriented tetrahedra (see ).
A motion of the first kind (orientation-preserving), different from a rotation and a translation, is the product of a translation and a rotation the axis of which is parallel to the direction of the translation (a so-called screwing motion). The theorem was proved by M. Chasles in 1830.
References
| [1] | P.S. Modenov, "Analytic geometry" , Moscow (1969) (In Russian) |
Comments
Any book on linear algebra and analytic geometry can serve as a reference, since both theorems are easy exercises. Another result that also is called Chasles' theorem can be found in [a1]: If the polars of the vertices of a triangle (cf. Polar) do not coincide with the respectively opposite sides, then they meet these sides in three collinear points.
References
| [a1] | H.S.M. Coxeter, "Projective geometry" , Blaisdell (1964) |
Chasles theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chasles_theorem&oldid=32020