Osculation

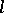of a curve with a curve at a given point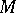

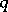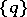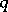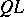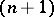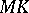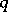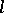A geometrical concept, meaning that has contact of maximal order with at in comparison with any curve in some given family of curves including . The order of contact of and is said to be equal to if the segment is a variable of -st order of smallness with respect to (see Fig., where is perpendicular to the common tangent of and at ).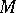

Figure: o070590a

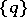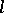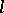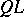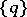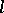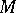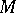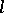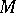Thus, of all the curves in , the curve having osculation with is the one which is most closely adjacent to (that is, for which has maximal order of smallness). The curve in having osculation with at a given point is called the osculating curve of the given family at this point. E.g., the osculating circle of at is the circle having maximal order of contact with at in comparison with any other circle.

Similarly one can define the concept of osculation of a surface 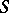in a given family of surfaces 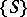with a curve 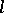(or with a surface) at some point 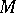of it. Here the order of contact is defined similarly, except that one must examine the tangent plane of 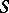at 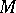instead of the tangent line 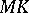in the figure.

References

[1]	V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1 , MIR (1982) (Translated from Russian)
[2]	P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)
[3]	J. Favard, "Cours de géométrie différentielle locale" , Gauthier-Villars (1957)
[4]	V.A. Zalgaller, "The theory of envelopes" , Moscow (1975) (In Russian)

Comments

The phrase "QL is a variable of the variable of n+1-st order of smallness with respect to another variablen+1-st order of smallness with respect to MK" means that 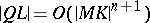as approaches .

References

[a1]	C.C. Hsiung, "A first course in differential geometry" , Wiley (1988) pp. Chapt. 2, Sect. 1.4