Cassini oval

A plane algebraic curve of order four whose equation in Cartesian coordinates has the form:

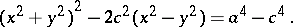Figure: c020700a

Figure: c020700b

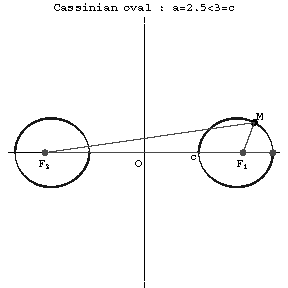
Figure: c020700c

A Cassini oval is the set of points (see Fig.) such that the product of the distances from each point to two given points and (the foci) is constant. When the Cassini oval is a convex curve; when it is a curve with "waists" (concave parts); when it is a Bernoulli lemniscate; and when it consists of two components. Cassini ovals are related to lemniscates. Cassini ovals were studied by G. Cassini (17th century) in his attempts to determine the Earth's orbit.

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)

Comments

A Cassini oval is also called a Cassinian oval.

References

[a1]	J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) MR1572089 Zbl 0257.50002
[a2]	J.W. Bruce, P.J. Giblin, "Curves and singularities: a geometrical introduction to singularity theory" , Cambridge Univ. Press (1984) MR1541053 Zbl 0534.58008