Barycentric subdivision

of a geometric complex

A complex obtained by replacing the simplices of by smaller ones by means of the following procedure. Each one-dimensional simplex (segment) is halved. On the assumption that all simplices of dimension 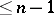are already subdivided, the subdivision of any -dimensional simplex is defined by means of cones over the simplices of the boundary of with a common vertex that is the barycentre of the simplex , i.e. the point with barycentric coordinates . The vertices of the resulting complex are in a one-to-one correspondence with the simplices of the complex , while the simplices of the complex are in such a correspondence with inclusion-ordered finite tuples of simplices from . The formal definition of a barycentric subdivision for the case of an abstract complex is analogous.

References

[a1]	K. Lamotke, "Semisimpliziale algebraische Topologie" , Springer (1968)