Endomorphism semi-group

A semi-group consisting of the endomorphisms of a certain object (a set 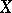endowed with some structure 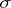) with the operation of multiplication (performing transformations in succession). The object 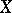can be a vector space, a topological space, an algebraic system, a graph, etc.; it is usually regarded as an object of a certain category, and as a rule, the morphisms (cf. Morphism) in this category are the mappings preserving the relations of 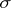(linear or continuous transformations, homomorphisms, etc.). The set 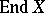of all endomorphism of 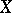(that is, of morphisms to its subobjects) is a sub-semi-group of the semi-group 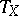of all transformations of 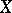(see Transformation semi-group).

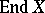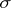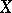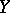The semi-group may include a considerable amount of information on the structure . For example, if and are vector spaces of dimensions 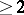over skew-fields 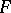and 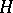, respectively, then if the semi-groups and 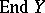of their endomorphisms (that is, linear transformations) are isomorphic, it follows that 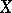and 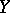(and in particular, 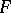and 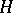) are isomorphic. Some pre-ordered sets and lattices, every Boolean ring, and some other algebraic systems are determined up to isomorphism by their endomorphism semi-groups. The same is true for some modules and transformation semi-groups. Similar information about 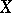is carried by certain proper sub-semi-groups of 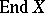(for example, the semi-groups of homeomorphic transformations of a topological space).

Some classes of objects 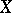(for example, topological spaces) can be characterized in this manner by their semi-groups of partial endomorphisms, that is, partial transformations of 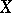that are morphisms of their subobjects.

References

[1]	L.M. Gluskin, "Transformation semigroups" , Proc. 4-th All-Union Math. Congress , 2 , Leningrad (1964) pp. 3–9 (In Russian)
[2]	A.A. Zykov, "The theory of finite graphs" , 1 , Novosibirsk (1969) (In Russian)
[3]	K.D. Magill, "A survey of semigroups of continuous selfmaps" Semigroup Forum , 11 (1975–1976) pp. 189–282
[4]	M. Petrich, "Rings and semigroups" , Springer (1974)