Operator-irreducible representation
From Encyclopedia of Mathematics
A representation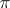 
of a group (algebra, ring, semi-group) 
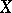on a (topological) vector space 
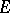such that any (continuous) linear operator on 
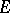commuting with every operator 
, 
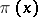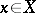, is a scalar multiple of the identity operator on 
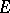. If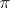 
is a completely-irreducible representation (in particular, if 
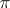is a finite-dimensional irreducible representation), then 
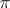is an operator-irreducible representation; the converse is not always true. If 
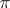is a unitary representation of a group or a symmetric representation of a symmetric algebra, then 
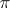is an operator-irreducible representation if and only if 
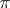is an irreducible representation.
Comments
References
| [a1] | I.M. Gel'fand, M.I. Graev, N.Ya. Vilenkin, "Generalized functions" , 5. Integral geometry and representation theory , Acad. Press (1966) pp. 149 ff (Translated from Russian) |
| [a2] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) pp. 114 (Translated from Russian) |
How to Cite This Entry:
Operator-irreducible representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator-irreducible_representation&oldid=31668
Operator-irreducible representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator-irreducible_representation&oldid=31668
This article was adapted from an original article by A.I. Shtern (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article