Snake-like continuum

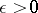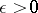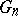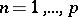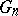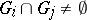A continuum which, for any , admits an open covering whose nerve (cf. Nerve of a family of sets) is a finite linear complex. In other words, for any the continuum must be covered by a finite system , , of open sets such that the diameter of each is less than and if and only if 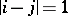(such a system is called an -chain). Every snake-like continuum is irreducible (see Irreducible continuum) between any pair of its points. Every subcontinuum of a snake-like continuum is snake-like. Two hereditarily-indecomposable snake-like continua (see Indecomposable continuum) containing more than one point are homeomorphic; these are known as pseudo-arcs (cf. Pseudo-arc). Every snake-like continuum is topologically imbeddable in the plane. Any homogeneous snake-like continuum is a pseudo-arc. Every snake-like continuum is the continuous image of a pseudo-arc and the limit of the inverse spectrum of arcs.

References

[1]	K. Kuratowski, "Topology" , 2 , Acad. Press (1968) (Translated from French)

Comments

A snake-like continuum is also called a chainable continuum.