Regular element
of a semi-group
An element  such that
such that 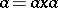 for some element
for some element  of the given semi-group; if in addition (for the same
of the given semi-group; if in addition (for the same  )
)  , then
, then  is called completely regular. If
is called completely regular. If  is a regular element of a semi-group
is a regular element of a semi-group 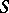 , then the principal right (left) ideal in
, then the principal right (left) ideal in 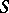 generated by
generated by  is generated by some idempotent; conversely, each of these symmetrical properties implies the regularity of
is generated by some idempotent; conversely, each of these symmetrical properties implies the regularity of  . If
. If 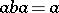 and
and 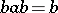 , the elements
, the elements  and
and 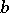 are called mutually inverse (also known as generalized inverse or regularly conjugate). Every regular element has an element inverse to it; generally speaking, it is not unique (see Inversion semi-group). Semi-groups in which any two elements are mutually inverse are in fact rectangular semi-groups (see Idempotents, semi-group of). Each completely-regular element
are called mutually inverse (also known as generalized inverse or regularly conjugate). Every regular element has an element inverse to it; generally speaking, it is not unique (see Inversion semi-group). Semi-groups in which any two elements are mutually inverse are in fact rectangular semi-groups (see Idempotents, semi-group of). Each completely-regular element  has an element inverse to it that commutes with
has an element inverse to it that commutes with  . An element is completely regular if and only if it belongs to some subgroup of a semi-group (cf. Clifford semi-group). For regular
. An element is completely regular if and only if it belongs to some subgroup of a semi-group (cf. Clifford semi-group). For regular  -classes, see Green equivalence relations.
-classes, see Green equivalence relations.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
Comments
A semi-group consisting completely of regular elements is a regular semi-group.
Regular element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_element&oldid=31596