Neuwirth knot

A polynomial knot 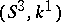(cf. Knot theory) whose group has a finitely-generated commutator subgroup. The complement 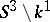of a Neuwirth knot is a fibre space over a circle and the fibre 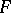is a connected surface whose genus is that of the knot. The commutator subgroup 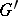of the group 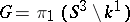of a Neuwirth knot is a free group of rank 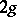, where is the genus of the knot. The coefficient of the leading term of the Alexander polynomial of a Neuwirth knot (cf. Alexander invariants) is 1 and the degree of this polynomial is . 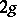All torus knots (cf. Torus knot) are Neuwirth knots. So is every alternating knot whose Alexander polynomial has leading coefficient .

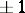These knots were introduced by L. Neuwirth (see [1]).

References

[1]	L.P. Neuwirth, "Knot groups" , Princeton Univ. Press (1965)