Knot table

The list of diagrams of all simple knots admitting a projection on the plane with 9 or fewer double points. The notation for the knots in this table is standard; the first number indicates the number of double points and the second (placed as a suffix) the ordinal number of the knot. E.g., the knot 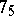is the fifth knot in the table with 7 intersections. Alongside each knot in coded form is given its Alexander polynomial 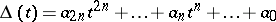(cf. Alexander invariants). Since the Alexander polynomial of every knot has even degree and is reciprocal (i.e. 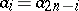), it suffices to give the set of last coefficients ; they are indicated in the table. 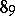E.g., next to the knot is written 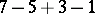. This means that the Alexander polynomial equals 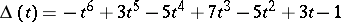. Non-alternating knots are marked by an asterisk (cf. Alternating knots and links). The table is taken from [1] with minor modifications.

Figure: k055590a

References

[1]	G. Burde, "Knoten" , Jahrbuch Ueberblicke Mathematik , B.I. Wissenschaftsverlag Mannheim (1978) pp. 131–147

Comments

A table of knots with up to 10 crossings can be found in [a1].

References

[a1]	D. Rolfsen, "Knots and links" , Publish or Perish (1976)