Struve function

The function

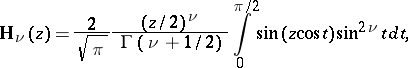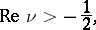that satisfies the inhomogeneous Bessel equation:

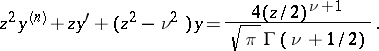The power series expansion is:

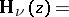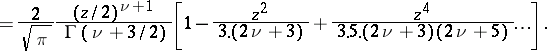A Struve function of integral order is related to a Weber function by the following relations:

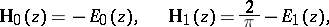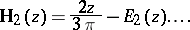A Struve function of order 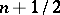( an integer) is an elementary function, for example

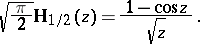When 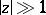, 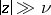the asymptotic expansion

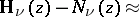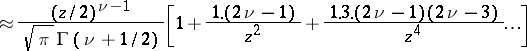holds, where 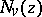is a Neumann function.

A modified Struve function is the function

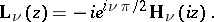Its series expansion is:

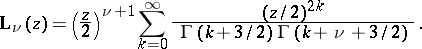For large 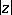, the asymptotic expansion

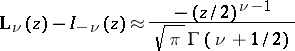holds, where 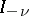is a modified Bessel function (cf. Bessel functions).

A Struve function is sometimes denoted by 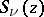. Introduced by H. Struve [1].

References

[1]	H. Struve, Ann. Physik Chemie , 17 (1882) pp. 1008–1016
[2]	E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966)
[3]	M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1970)

Comments

The Struve function can be expressed in terms of a hypergeometric function of type 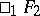, cf. [a1], formula (7.5).

References

[a1]	H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953)
[a2]	G.N. Watson, "A treatise on the theory of Bessel functions" , 1 , Cambridge Univ. Press (1952)