Multiplicative arithmetic function
An arithmetic function of one argument,  , satisfying the condition
, satisfying the condition
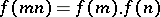 | (*) |
for any pair of coprime integers  . It is usually assumed that
. It is usually assumed that  is not identically zero (which is equivalent to the condition
is not identically zero (which is equivalent to the condition 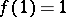 ). A multiplicative arithmetic function is called strongly multiplicative if
). A multiplicative arithmetic function is called strongly multiplicative if  for all prime numbers
for all prime numbers  and all natural numbers
and all natural numbers 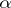 . If (*) holds for any two numbers
. If (*) holds for any two numbers 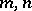 , and not just for coprime numbers, then
, and not just for coprime numbers, then  is called totally multiplicative; in this case
is called totally multiplicative; in this case  .
.
Examples of multiplicative arithmetic functions. The function 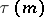 , the number of natural divisors of a natural number
, the number of natural divisors of a natural number  ; the function
; the function  , the sum of the natural divisors of the natural number
, the sum of the natural divisors of the natural number 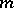 ; the Euler function
; the Euler function 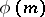 ; and the Möbius function
; and the Möbius function 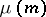 . The function
. The function 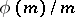 is a strongly-multiplicative arithmetic function, a power function
is a strongly-multiplicative arithmetic function, a power function 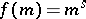 is a totally-multiplicative arithmetic function.
is a totally-multiplicative arithmetic function.
Comments
The convolution product
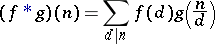 |
yields a group structure on the multiplicative functions. The unit element is given by the function  , where
, where  and
and  for all
for all  . Another standard multiplicative function is the constant function
. Another standard multiplicative function is the constant function  (
(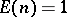 for all
for all 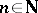 ) and its inverse
) and its inverse 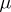 , the Möbius function. Note that
, the Möbius function. Note that 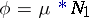 , where
, where 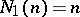 for all
for all  , and that
, and that 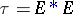 ,
,  .
.
Formally, the Dirichlet series of a multiplicative function 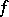 has an Euler product:
has an Euler product:
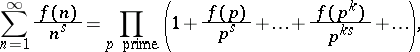 |
whose form simplifies considerably if  is strongly or totally multiplicative.
is strongly or totally multiplicative.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1960) pp. Chapts. XVI-XVII |
Multiplicative arithmetic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplicative_arithmetic_function&oldid=30082