Borel system of sets
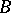 -system, generated by a system of sets
-system, generated by a system of sets 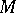
The smallest 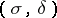 -system of sets,
-system of sets, 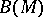 , containing
, containing 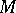 . The sets belonging to
. The sets belonging to 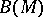 are called the Borel sets (cf. Borel set), or
are called the Borel sets (cf. Borel set), or 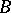 -sets, generated by the system
-sets, generated by the system  . For each ordinal number
. For each ordinal number 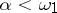 , where
, where  is the initial ordinal number of cardinality
is the initial ordinal number of cardinality 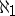 , the Borel classes
, the Borel classes 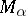 are defined as follows:
are defined as follows: 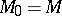 ;
; 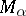 consists of the unions if
consists of the unions if 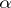 is odd, and it consists of the intersections if
is odd, and it consists of the intersections if 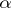 is even, of sequences of sets belonging to
is even, of sequences of sets belonging to 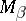 ,
, 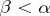 . In such a case
. In such a case 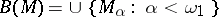 . The same Borel system of sets
. The same Borel system of sets 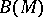 is obtained if the union and intersection above are interchanged. A Borel set belongs properly to a class
is obtained if the union and intersection above are interchanged. A Borel set belongs properly to a class 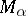 if it belongs to the class
if it belongs to the class 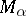 but does not belong to
but does not belong to 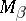 if
if 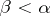 . (Sometimes one takes non-intersecting classes, i.e. then the system
. (Sometimes one takes non-intersecting classes, i.e. then the system 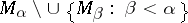 is called a class.)
is called a class.)
Borel system of sets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_system_of_sets&oldid=29890