Convolution of functions

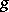and belonging to

The function defined by

it is denoted by the symbol . The function is defined almost everywhere and also belongs to . The convolution has the basic properties of multiplication, namely,

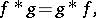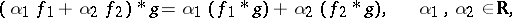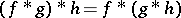for any three functions in 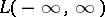. Therefore, with the usual operations of addition and of multiplication by a scalar, with the operation of convolution as the multiplication of elements, and with the norm

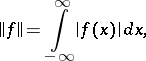is a Banach algebra (for this norm ). If denotes the Fourier transform of , then

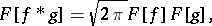and this is used in solving a number of applied problems.

Thus, if a problem has been reduced to an integral equation of the form

(*)

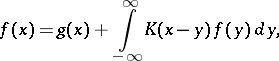where

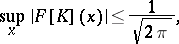then, under the assumption that , by applying the Fourier transformation to (*) one obtains

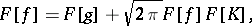hence

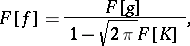and the inverse Fourier transformation yields the solution to (*) as

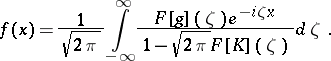The properties of a convolution of functions have important applications in probability theory. If and are the probability densities of independent random variables and , respectively, then is the probability density of the random variable .

The convolution operation can be extended to generalized functions (cf. Generalized function). If and 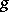are generalized functions such that at least one of them has compact support, and if is a test function, then is defined by

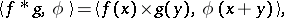where is the direct product of 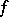and , that is, the functional on the space of test functions of two independent variables given by

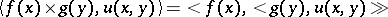for every infinitely-differentiable function of compact support.

The convolution of generalized functions also has the commutativity property and is linear in each argument; it is associative if at least two of the three generalized functions have compact supports. The following equalities hold:

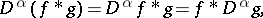where is the differentiation operator and is any multi-index,

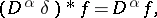in particular, 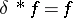, where denotes the delta-function. Also, if 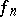, 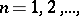are generalized functions such that 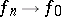, and if there is a compact set 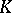such that

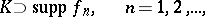then

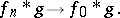Finally, if 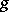is a generalized function of compact support and is a generalized function of slow growth, then the Fourier transformation can be applied to , and again

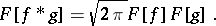The convolution of generalized functions is widely used in solving boundary value problems for partial differential equations. Thus, the Poisson integral, written in the form

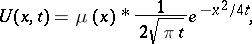is a solution to the thermal-conductance equation for an infinite bar, where the initial temperature can be not only an ordinary function but also a generalized one.

Both for ordinary and generalized functions the concept of a convolution carries over in a natural way to functions of several variables; then in the above and must be regarded as vectors from and not as real numbers.

References

[1]	V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) MR0764399 Zbl 0954.35001 Zbl 0652.35002 Zbl 0695.35001 Zbl 0699.35005 Zbl 0607.35001 Zbl 0506.35001 Zbl 0223.35002 Zbl 0231.35002 Zbl 0207.09101
[2]	I.M. Gel'fand, G.E. Shilov, "Generalized functions" , 1–5 , Acad. Press (1964) (Translated from Russian) MR435831 Zbl 0115.33101
[3]	E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) MR0942661 Zbl 0017.40404 Zbl 63.0367.05

References

[a1]	W. Kecs, "The convolution product and some applications" , Reidel & Ed. Academici (1982) MR0690953 Zbl 0512.46041