Integration by substitution

change of variable in an integral

One of the methods for calculating an integral. It consists in transforming the integral by transition to another variable of integration. For the definite integral of a function of one variable the formula is

(1)

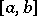It is true under the assumptions: is continuous on the interval , which is the range of a function 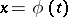that is defined and continuous, together with its first derivative 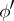, on an interval 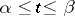, and , .

The analogue of (1) for the indefinite integral is

(2)

If is defined and differentiable on some segment 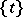, while 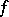has a primitive on the range of 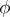, then 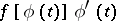also has a primitive on the given segment, and (2) holds.

In the case of a multiple Riemann integral over a bounded closed 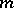-dimensional measurable region 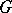(cf. Multiple integral), the analogue of (1) is

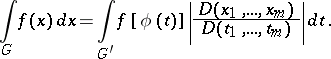(3)

Formula (3) holds under the following assumptions: the function 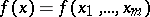is continuous in ; the transformation 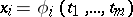, , maps a region in the space of variables 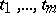one-to-one onto 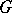; the functions have in 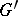continuous first-order partial derivatives, and their Jacobian 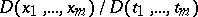does not vanish. Formula (3) holds under more general assumptions as well (it is not necessary to require that 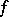be continuous in 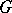, and the Jacobian may vanish on a set of 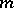-dimensional measure zero).

References

[1]	V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian)
[2]	L.D. Kudryavtsev, "Mathematical analysis" , 1–2 , Moscow (1970) (In Russian)
[3]	S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian)

Comments

For very general hypothesis under which (1) and (3) hold for Lebesgue integrals (cf. Lebesgue integral) see [a1].

For additional references see also Improper integral.

References

[a1]	K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981)