Lebesgue criterion

A criterion for pointwise convergence of Fourier series. If a 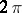-periodic function , integrable on the interval 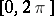, satisfies the condition

(*)

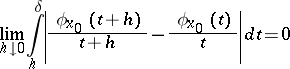at a point for some 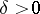, where

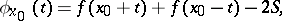then the Fourier series of 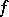at converges to the number 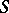. The criterion was proved by H. Lebesgue [1]. Condition (*) is equivalent to the aggregate of the two conditions

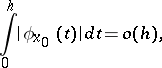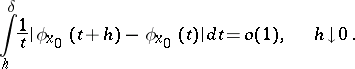The Lebesgue criterion is more powerful then the Dirichlet criterion (convergence of series); the Jordan criterion; the Dini criterion; the de la Vallée-Poussin criterion; and the Young criterion.

References

[1]	H. Lebesgue, "Récherches sur le convergence des séries de Fourier" Math. Ann. , 61 (1905) pp. 251–280
[2]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)

References

[a1]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988)