Hausdorff measure

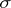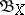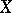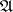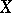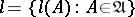A collective name for the class of measures determined on the Borel -algebra of a metric space by means of the following construction: Let be a certain class of open subsets of , let be a non-negative function defined on 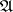, and let

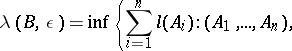where the infimum is taken over all finite or countable coverings of the Borel set by sets in 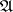with diameter not exceeding . The Hausdorff measure 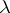defined by the class 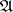and the function 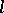is the limit

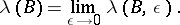Examples of Hausdorff measures. 1) Let 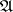be the collection of all balls in 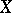, and let 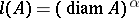, 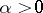. The corresponding measure 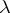is called the Hausdorff 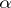-measure (the linear Hausdorff measure for 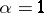and the plane Hausdorff measure for 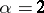). 2) Let 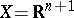, and let 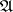be the collection of cylinders with spherical bases and with axes parallel to the direction of the axis 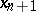; let 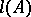be the -dimensional volume of the axial section of a cylinder 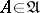; the corresponding Hausdorff measure is called the cylindrical measure.

The Hausdorff measures were introduced by F. Hausdorff [1].

References

[1]	F. Hausdorff, "Dimension and äusseres Mass" Math. Ann. , 79 (1918) pp. 157–179 MR1511917
[2]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523

Comments

A method to construct measures on metric spaces was introduced by C. Carathéodory in 1914. The elements of 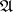can be anything and are often taken closed. The Hausdorff measures are -additive on the Borel 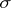-field, but are in general not 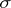-finite; some restrictions on 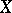, 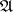and 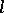have to be added in order to get nice properties of approximation from below. Such restrictions are, e.g., 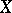is a Borel subset of some compact metric space, 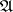is the class of closed subsets of and 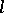is of the form 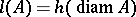where 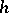is a continuous non-decreasing function from 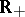to 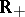. The measures obtained in this way are the Hausdorff measures most often used, and were mainly studied by A.S. Besicovitch and his school (cf. [a8]); they are called (Hausdorff) 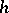-measures (if 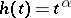, , 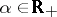one says 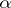-measure or 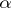-dimensional measure; see also Hausdorff dimension). 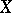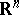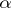When is the Euclidean space , the -dimensional measure is equal (up to a multiplicative constant) to the Lebesgue measure if and, when restricted to smooth curves, surfaces, etc., is equal to the length, area, etc. if 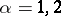, etc. The -measure is the counting measure, which is also at the confines of potential theory and descriptive set theory.

Even though the notion of Hausdorff measure is not regarded as being fundamental, it appears in many parts of hard analysis and geometry. Through the study of exceptional sets, it is used, for example, in harmonic analysis (cf. [a5]), in potential theory (cf. [a1]), in the metric theory of continued fractions (cf. [a8]), and in differential geometry (cf. Sard theorem). For many reasons it is closely linked to the notion of capacity, and, more generally, to descriptive set theory (cf. [a1], [a2], [a8]; R.O. Davies was, before G. Choquet, the first to prove capacitability theorems). In the theory of stochastic processes it has a crucial role in the fine study of the paths of the Wiener process and others (cf. [a6] and its bibliography). 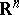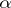Finally, on , the -dimensional measure is, when is a natural integer, a fundamental notion in geometric measure theory (cf. Area; Minimal surface, and [a4] in which also Hausdorff measures which are not 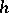-measures (Favard measure, etc.) are used); for non-integer 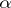it is a fundamental notion in the theory of fractals (cf. [a3]).

For the use of Hausdorff measures and the Hausdorff dimension in multi-dimensional complex analysis, see, e.g., [a9].

References

[a1]	L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) MR0225986 Zbl 0189.10903
[a2]	C. Dellacherie, "Ensembles analytiques, capacités, mesures de Hausdorff" , Lect. notes in math. , 295 , Springer (1972) MR0492152 Zbl 0259.31001
[a3]	K.J. Falconer, "The geometry of fractal sets" , Cambridge Univ. Press (1985) MR0867284 Zbl 0587.28004
[a4]	H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 MR0257325 Zbl 0176.00801
[a5]	J.-P. Kahane, R. Salem, "Ensembles parfaits et séries trigonométriques" , Hermann (1963) pp. 142 MR0160065 Zbl 0112.29304
[a6]	J.-F. le Gall, "Temps locaux d'intersection et points multiples des processus de Lévy" , Sem. Probab. XXI , Lect. notes in math. , 1247 , Springer (1987) pp. 341–374 Zbl 0621.60077
[a7]	M.E. Munroe, "Introduction to measure and integration" , Addison-Wesley (1953) pp. 111 MR1528565 MR0053186 Zbl 0050.05603
[a8]	C.A. Rogers, "Hausdorff measures" , Cambridge Univ. Press (1970) MR0281862 Zbl 0204.37601
[a9]	E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian) MR1111477 Zbl 0683.32002