Weak topology

The locally convex topology on a vector space 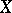generated by the family of semi-norms (cf. Semi-norm) 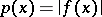, where 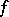ranges over some subset 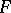of the (algebraic) adjoint space .

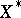References

[1]	L.A. Lyusternik, V.I. Sobolev, "A short course of functional analysis" , Moscow (1982) (In Russian)
[2]	H.H. Schaefer, "Topological vector spaces" , Springer (1971)

Comments

The weak topology as introduced above is often denoted by 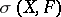. It is a Hausdorff topology if and only if 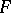separates the points of .

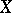See also Strong topology.

References

[a1]	H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German)