Scherk surface

A minimal surface obtained by H. Scherk in 1834. It is defined by the equation and it is the only minimal surface that can be represented as a translation surface of the form . Scherk's surface and its modifications are used for the construction of auxiliary functions that allow one to find examples of the unsolvability of the Dirichlet problem for the Euler–Lagrange equation for minimal surfaces over non-convex domains.

Scherk's surface possesses a number of interesting properties: it is a complete surface of infinite genus containing a countable number of straight lines; its universal covering surface presents an example of a complete minimal surface of conformally-hyperbolic type; and its spherical image does not contain exactly the four points and . The last property of Scherk's surface becomes evident from its representation by the Weierstrass formula, in which , , where varies in the plane with four deleted points and . By analogy with this representation one may construct the generalized Scherk surfaces

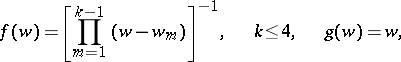which are complete minimal surfaces the normals to which "omit" exactly , , 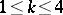of any pre-assigned directions. The existence of such minimal surfaces is interesting in connection with the conjecture that there are no complete minimal surfaces whose normals "omit" more than four directions. Such a conjecture has been proved (1984) for a number of directions greater than seven.

Scherk's surface belongs to the family of so-called periodic minimal surfaces; a picture of it, and other interesting properties, can be found in [1].

References

[1]	A.A. Tuzhilin, A.T. Fomenko, "Elements of the geometry and topology of minimal surfaces" , Moscow (1991) (In Russian)

References

[a1]	D.J. Struik, "Differential geometry" , Addison-Wesley (1957)
[a2]	J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975) pp. §455