Mass and co-mass
Adjoint norms (cf. Norm) in certain vector spaces dual to each other.
1) The mass of an  -vector
-vector 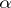 , i.e. an element of the
, i.e. an element of the  -fold exterior product of a vector space, is the number
-fold exterior product of a vector space, is the number
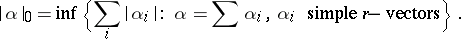 |
The co-mass of an  -covector
-covector 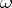 is the number
is the number
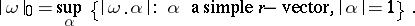 |
Here  is the standard norm of an
is the standard norm of an  -vector and
-vector and 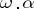 is the scalar product of a vector and a covector.
is the scalar product of a vector and a covector.
The mass 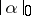 and the co-mass
and the co-mass 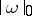 are adjoint norms in the spaces of
are adjoint norms in the spaces of  -vectors
-vectors 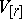 and
and  -covectors
-covectors 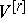 , respectively. In this connection:
, respectively. In this connection:
a) 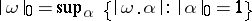 ,
, 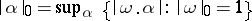 ;
;
b) 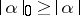 ,
, 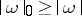 , and equalities hold if and only if
, and equalities hold if and only if 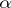 (
(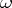 ) is a simple
) is a simple  -(co)vector;
-(co)vector;
c) 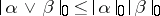 ,
, 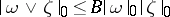 for exterior products
for exterior products 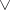 , where for a simple multi-covector
, where for a simple multi-covector 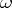 (or
(or 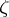 )
) 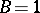 , and, in general,
, and, in general,  if
if 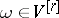 and
and 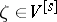 ;
;
d) 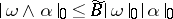 for inner products
for inner products  , where
, where 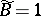 for
for 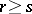 and
and 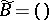 for
for 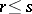 ,
,  and
and 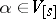 .
.
These definitions enable one to define the mass and co-mass for sections of fibre bundles whose standard fibres are 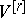 and
and 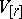 . For example, the co-mass of a form
. For example, the co-mass of a form 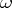 on a domain
on a domain  is
is
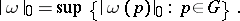 |
2) The mass of a polyhedral chain 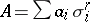 is
is
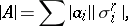 |
where 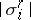 is the volume of the cell
is the volume of the cell 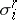 . For arbitrary chains the mass (finite or infinite) can be defined in various ways; for flat chains (see Flat norm) and sharp chains (see Sharp norm) these give the same value to the mass.
. For arbitrary chains the mass (finite or infinite) can be defined in various ways; for flat chains (see Flat norm) and sharp chains (see Sharp norm) these give the same value to the mass.
3) The co-mass of a (flat, in particular, sharp) cochain 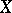 is defined in the standard way:
is defined in the standard way:
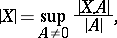 |
where 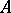 is a polyhedral chain and
is a polyhedral chain and 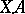 is the value of the cochain
is the value of the cochain 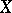 on the chain
on the chain 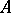 .
.
For references see Flat norm.
Comments
A simple  -vector
-vector 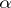 is an element of the form
is an element of the form 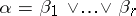 in the
in the  -fold exterior product
-fold exterior product 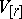 of a vector space
of a vector space 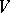 . Here "" denotes exterior product and
. Here "" denotes exterior product and 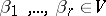 .
.
References
| [a1] | H. Federer, "Geometric measure theory" , Springer (1969) pp. Sect. 1.8 |
Mass and co-mass. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mass_and_co-mass&oldid=28243