Gradient

One of the fundamental concepts in vector analysis and the theory of non-linear mappings.

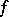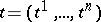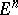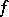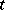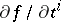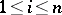The gradient of a scalar function of a vector argument from a Euclidean space is the derivative of with respect to the vector argument , i.e. the -dimensional vector with components , . The following notations exist for the gradient of 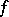at :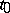

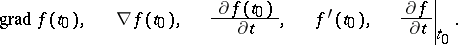The gradient is a covariant vector: the components of the gradient, computed in two different coordinate systems 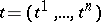and 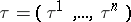, are connected by the relations:

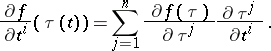The vector 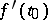, with its origin at 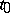, points to the direction of fastest increase of 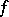, and is orthogonal to the level lines or surfaces of 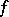passing through .

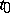The derivative of the function at 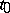in the direction of an arbitrary unit vector 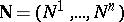is equal to the projection of the gradient function onto this direction:

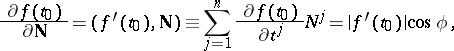(1)

where 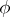is the angle between 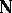and 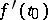. The maximal directional derivative is attained if 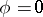, i.e. in the direction of the gradient, and that maximum is equal to the length of the gradient.

The concept of a gradient is closely connected with the concept of the differential of a function. If 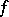is differentiable at 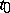, then, in a neighbourhood of that point,

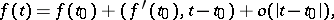(2)

i.e. 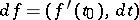. The existence of the gradient of 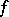at 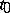is not sufficient for formula (2) to be valid.

A point 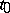at which 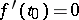is called a stationary (critical or extremal) point of 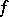. An example of such a point is a local extremal point of 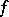, and the system 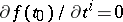, , 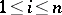is employed to find an extremal point .

The following formulas can be used to compute the value of the gradient:

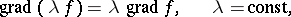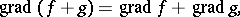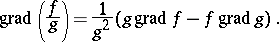The gradient 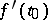is the derivative at 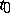with respect to volume of the vector function given by

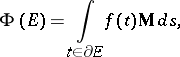where 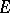is a domain with boundary 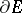, , 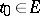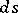is the area element of 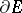, and 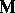is the unit vector of the outward normal to 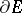. In other words,

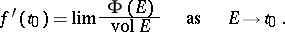Formulas (1), (2) and the properties of the gradient listed above indicate that the concept of a gradient is invariant with respect to the choice of a coordinate system.

In a curvilinear coordinate system 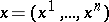, in which the square of the linear element is

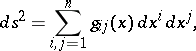the components of the gradient of 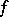with respect to the unit vectors tangent to coordinate lines at are

where the matrix 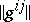is the inverse of the matrix .

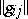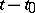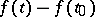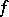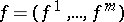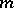The concept of a gradient for more general vector functions of a vector argument is introduced by means of equation (2). Thus, the gradient is a linear operator the effect of which on the increment of the argument is to yield the principal linear part of the increment of the vector function . E.g., if is an -dimensional vector function of the argument 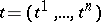, then its gradient at a point 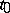is the Jacobi matrix 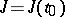with components 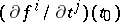, , 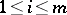, 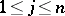and

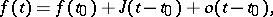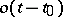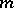where is an -dimensional vector of length 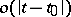. The matrix 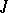is defined by the limit transition

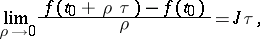(3)

for any fixed -dimensional vector .

In an infinite-dimensional Hilbert space definition (3) is equivalent to the definition of differentiability according to Fréchet, the gradient then being identical with the Fréchet derivative.

If the values of 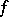lie in an infinite-dimensional vector space, various types of limit transitions in (3) are possible (see, for example, Gâteaux derivative).

In the theory of tensor fields on a domain of an -dimensional affine space with a connection, the gradient serves to describe the principal linear part of increment of the tensor components under parallel displacement corresponding to the connection. The gradient of a tensor field

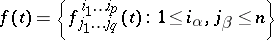of type 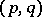is the tensor of type 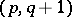with components

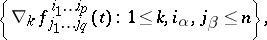where 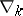is the operator of absolute (covariant) differentiation (cf. Covariant differentiation).

The concept of a gradient is widely employed in many problems in mathematics, mechanics and physics. Many physical fields can be regarded as gradient fields (cf. Potential field).

References

[1]	N.E. Kochin, "Vector calculus and fundamentals of tensor calculus" , Moscow (1965) (In Russian)
[2]	P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)

References

[a1]	W. Fleming, "Functions of several variables" , Addison-Wesley (1965)