Positive variation of a function
From Encyclopedia of Mathematics
One of the two terms whose sum is the complete change, or (total) variation, of the function (cf. Variation of a function) over a given interval. Let 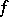 be a function of a real variable given on the segment
be a function of a real variable given on the segment 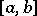 and taking real values. Let
and taking real values. Let 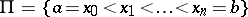 be any partition of
be any partition of 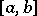 and let
and let
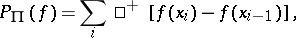 |
where the summation is over those values of 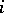 for which the difference
for which the difference 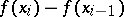 is non-negative. The quantity
is non-negative. The quantity
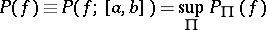 |
is called the positive variation of the function 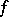 over
over 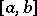 . Of course,
. Of course,  . The concept of the positive variation of a function was introduced by C. Jordan [1]. See also Negative variation of a function.
. The concept of the positive variation of a function was introduced by C. Jordan [1]. See also Negative variation of a function.
References
| [1] | C. Jordan, "Sur la série de Fourier" C.R. Acad. Sci. Paris , 92 (1881) pp. 228–230 |
| [2] | H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) |
How to Cite This Entry:
Positive variation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_variation_of_a_function&oldid=27950
Positive variation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_variation_of_a_function&oldid=27950
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article