Regular measure
From Encyclopedia of Mathematics
A measure defined on the Borel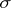 
-algebra 
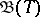of a topological space 
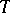such that for any Borel set 
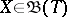and any 
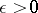there is an open set 
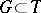containing 
, 
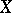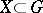, and such that 
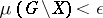. An equivalent definition is as follows: For any 
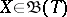and any 
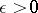there is a closed set 
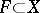such that 
.
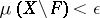Comments
See also Regular set function.
This notion of regular measure should not be confused with that of a regular outer measure, which is an outer measure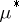 
(cf. also Measure) such that for every 
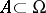there is a measurable set 
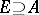such that 
.
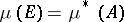References
| [a1] | M.E. Munroe, "Introduction to measure and integration" , Addison-Wesley (1953) pp. 111 |
How to Cite This Entry:
Regular measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_measure&oldid=27568
Regular measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_measure&oldid=27568
This article was adapted from an original article by R.A. Minlos (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article