Linear interpolation
From Encyclopedia of Mathematics
A method for the approximate calculation of the value of a function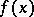 
, based on the replacement of 
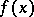by a linear function
 |
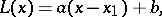the parameters 
and 
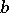being chosen in such a way that the values of 
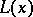coincide with the values of 
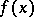at given points 
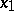and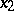 
:
 |
These conditions are satisfied by the unique function
 |
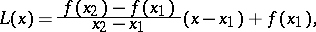which approximates the given function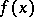 
on the interval 
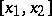with error
 |
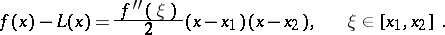The calculations necessary for linear interpolation are easily realized by hand; for this reason this method is widely used for the interpolation of tabular data.
References
| [1] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [2] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
Comments
References
| [a1] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126 |
| [a2] | J.F. Steffensen, "Interpolation" , Chelsea, reprint (1950) |
How to Cite This Entry:
Linear interpolation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_interpolation&oldid=27067
Linear interpolation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_interpolation&oldid=27067
This article was adapted from an original article by M.K. Samarin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article