Abel summation method
One of the methods for the summation of series of numbers. The series
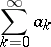 |
can be summed by the Abel method ( -method) to the number
-method) to the number  if, for any real
if, for any real  ,
,  , the series
, the series
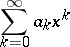 |
is convergent and
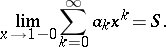 |
This summation method can already be found in the works of L. Euler and G. Leibniz. The name "Abel summation method" originates from the Abel theorem on the continuity of power series. The Abel summation method belongs to the class of totally regular summation methods and is more powerful than the entire set of Cesàro summation methods. The Abel summation method is used in conjunction with Tauberian theorems to demonstrate the convergence of a series.
A closely related summation method is the  -method. Let
-method. Let  be a complex number,
be a complex number, 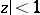 ; the series
; the series
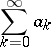 |
is summed by the 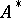 -method to the number
-method to the number 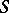 if
if
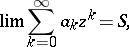 |
where 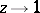 along any path not tangent to the unit circle.
along any path not tangent to the unit circle.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
Abel summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_summation_method&oldid=26200