Trace of a square matrix
From Encyclopedia of Mathematics
The sum of the entries on the main diagonal of this matrix. The trace of a matrix 
is denoted by 
, 
or 
:
 |
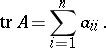Let 
be a square matrix of order 
over a field 
. The trace of 
coincides with the sum of the roots of the characteristic polynomial of 
. If 
is a field of characteristic 0, then the 
traces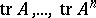 
uniquely determine the characteristic polynomial of 
. In particular, 
is nilpotent if and only if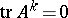 
for all 
.
If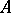 
and 
are square matrices of the same order over 
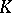, and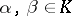 
, then
 |
 |
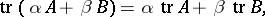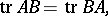while if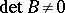 
,
 |
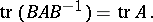The trace of the tensor (Kronecker) product of square matrices over a field is equal to the product of the traces of the factors.
Comments
References
| [a1] | P.M. Cohn, "Algebra" , 1 , Wiley (1982) pp. 336 |
| [a2] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1959) (Translated from Russian) |
How to Cite This Entry:
Trace of a square matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trace_of_a_square_matrix&oldid=25902
Trace of a square matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trace_of_a_square_matrix&oldid=25902
This article was adapted from an original article by D.A. Suprunenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article