Jet
From Encyclopedia of Mathematics
A polynomial  obtained by the truncation of the (formal) Taylor series of a differentiable function
obtained by the truncation of the (formal) Taylor series of a differentiable function 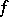 . More precisely, let
. More precisely, let 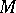 and
and 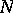 be
be 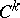 -manifolds. The class
-manifolds. The class 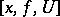 of equivalent triples
of equivalent triples 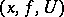 , where
, where 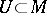 is open,
is open, 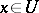 ,
,  is a mapping of class
is a mapping of class 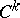 , is then called a
, is then called a 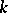 -jet from
-jet from 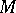 to
to 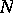 . Equivalence is defined thus:
. Equivalence is defined thus:
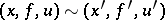 |
if 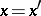 and if the local images of the mappings
and if the local images of the mappings 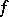 ,
, 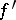 at
at  in relation to a pair of charts have identical derivatives up to the order
in relation to a pair of charts have identical derivatives up to the order 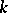 , inclusive. The space of jets
, inclusive. The space of jets 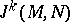 is a
is a 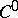 -manifold.
-manifold.
References
| [1] | P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) MR0494220 Zbl 0302.58006 |
| [2] | W. Guillemin, "Stable mappings and their singularities" , Springer (1973) MR0341518 Zbl 0294.58004 |
| [3] | T. Poston, I. Stewart, "Catastrophe theory and its applications" , Pitman (1978) MR0501079 Zbl 0382.58006 |
How to Cite This Entry:
Jet. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jet&oldid=25769
Jet. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jet&oldid=25769
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article