Talk:Gamma-function

$\Gamma$-function

$ \newcommand{\Re}{\mathop{\mathrm{Re}}} $

A transcendental function $\Gamma(z)$ that extends the values of the factorial $z!$ to any complex number $z$. It was introduced in 1729 by L. Euler in a letter to Ch. Goldbach, using the infinite product $$ \Gamma(z) = \lim_{n\rightarrow\infty}\frac{n!n^z}{z(z+1)\ldots(z+n)} = \lim_{n\rightarrow\infty}\frac{n^z}{z(1+z/2)\ldots(1+z/n)}, $$ which was used by L. Euler to obtain the integral representation (Euler integral of the second kind, cf. Euler integrals) $$ \Gamma(z) = \int_0^\infty x^{z-1}e^{-x} \rd x, $$ which is valid for $\Re z > 0$. The multi-valuedness of the function $x^{z-1}$ is eliminated by the formula $x^{z-1}=e^{(z-1)\ln x}$ with a real $\ln x$. The symbol $\Gamma(z)$ and the name gamma-function were proposed in 1814 by A.M. Legendre.

If $\Re z < 0$ and $-k-1 < \Re z < -k$, $k=0,1,\ldots$, the gamma-function may be represented by the Cauchy–Saalschütz integral: $$ \Gamma(z) = \int_0^\infty x^{z-1} \left( e^{-x} - \sum_{m=0}^k (-1)^m \frac{x^m}{m!} \right) \rd x. $$ In the entire plane punctured at the points $z=0,-1,\ldots $, the gamma-function satisfies a Hankel integral representation: $$ \Gamma(z) = \frac{1}{e^{2\pi iz} - 1} \int_C s^{z-1}e^{-s} \rd s, $$ where $s^{z-1} = e^{(z-1)\ln s}$ and $\ln s$ is the branch of the logarithm for which $0 < \arg\ln s < 2\pi$; the contour $C$ is represented in Fig. a. [FIXME] It is seen from the Hankel representation that $\Gamma(z)$ is a meromorphic function. At the points $z_n = -n$, $n=0,1,\ldots$ it has simple poles with residues $(-1)^n/n!$.

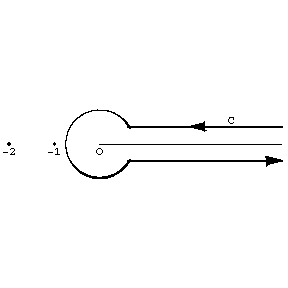
Figure: g043310a

Fundamental relations and properties of the gamma-function.

1) Euler's functional equation: $$ z\Gamma(z) = \Gamma(z+1), $$ or $$ \Gamma(z) = \frac{1}{z\ldots(z+n)}\Gamma(z+n+1); $$ $\Gamma(1)=1$, $\Gamma(n+1) = n!$ if $n$ is an integer; it is assumed that $0! = \Gamma(1) = 1$.

2) Euler's completion formula: $$ \Gamma(z)\Gamma(1-z) = \frac{\pi}{\sin \pi z}. $$ In particular, $\Gamma(1/2)=\sqrt{\pi}$; $$ \Gamma\left(n+\frac{1}{2}\right) = \frac{1.3\ldots(2n-1)}{2^n}\sqrt{\pi} $$ if $n>0$ is an integer; $$ \left| \Gamma\left(\frac{1}{2} + iy\right) \right|^2 = \frac{\pi}{\cosh y\pi}, $$ where $y$ is real.

3) Gauss' multiplication formula: $$ \prod_{k=0}^{m-1} \Gamma\left( z + \frac{k}{m} \right) = (2\pi)^{(m-1)/2}m^{(1/2)-mz}\Gamma(mz), \quad m = 2,3,\ldots $$ If $m=2$, this is the Legendre duplication formula.

4) If $ $ or $ $, then $ $ can be asymptotically expanded into the Stirling series:

$ $

$ $

where $ $ are the Bernoulli numbers. It implies the equality

$ $

$ $

In particular,

$ $

More accurate is Sonin's formula [6]:

$ $

5) In the real domain, $ $ for $ $ and it assumes the sign $ $ on the segments $ $, $ $ (Fig. b).

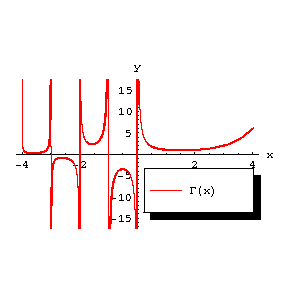
Figure: g043310b

The graph of the function $ $.

For all real $ $ the inequality

$ $

is valid, i.e. all branches of both $ $ and $ $ are convex functions. The property of logarithmic convexity defines the gamma-function among all solutions of the functional equation

$ $

up to a constant factor.

For positive values of $ $ the gamma-function has a unique minimum at $ $ equal to $ $. The local minima of the function $ $ form a sequence tending to zero as $ $.

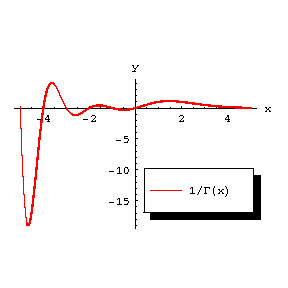
Figure: g043310c

The graph of the function $ $.

6) In the complex domain, if $ $, the gamma-function rapidly decreases as $ $,

$ $

7) The function $ $ (Fig. c) is an entire function of order one and of maximal type; asymptotically, as $ $,

$ $

where

$ $

It can be represented by the infinite Weierstrass product:

$ $

which converges absolutely and uniformly on any compact set in the complex plane ($ $ is the Euler constant). A Hankel integral representation is valid:

$ $

where the contour $ $ is shown in Fig. d.

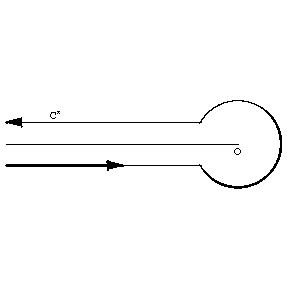
Figure: g043310d

$ $

G.F. Voronoi [7] obtained integral representations for powers of the gamma-function.

In applications, the so-called poly gamma-functions — $ $-th derivatives of $ $ — are of importance. The function (Gauss' $ $-function)

$ $

$ $

is meromorphic, has simple poles at the points $ $ and satisfies the functional equation

$ $

The representation of $ $ for $ $ yields the formula

$ $

where

$ $

This formula may be used to compute $ $ in a neighbourhood of the point $ $.

For other poly gamma-functions see [2]. Theincomplete gamma-function is defined by the equation

$ $

The functions $ $ and $ $ are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem).

The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series (see, for example, Beta-function). In addition, it is widely used in the theory of special functions (thehypergeometric function, of which the gamma-function is a limit case, cylinder functions, etc.), in analytic number theory, etc.

References

[1]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952)
[2]	H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953)
[3]	N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) (Translated from French)
[4]	, Math. anal., functions, limits, series, continued fractions , Handbook Math. Libraries , Moscow (1961) (In Russian)
[5]	N. Nielsen, "Handbuch der Theorie der Gammafunktion" , Chelsea, reprint (1965)
[6]	N.Ya. Sonin, "Studies on cylinder functions and special polynomials" , Moscow (1954) (In Russian)
[7]	G.F. Voronoi, "Studies of primitive parallelotopes" , Collected works , 2 , Kiev (1952) pp. 239–368 (In Russian)
[8]	E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)
[9]	A. Angot, "Compléments de mathématiques. A l'usage des ingénieurs de l'electrotechnique et des télécommunications" , C.N.E.T. (1957)

Comments

The $ $-analogue of the gamma-function is given by

$ $

$ $

cf. [a2]. Its origin goes back to E. Heine (1847) and D. Jackson (1904). For the gamma-function see also[a1].

References

[a1]	E. Artin, "The gamma function" , Holt, Rinehart & Winston (1964)
[a2]	R. Askey, "The $ $-Gamma and $ $-Beta functions" Appl. Anal. , 8 (1978) pp. 125–141