Principal ideal

An ideal (of a ring, algebra, semi-group, or lattice) generated by one element , i.e. the smallest ideal containing the element .

The left principal ideal of a ring contains, in addition to the element itself, also all the elements

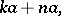the right principal ideal contains all the elements

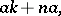and the two-sided principal ideal contains all elements of the form

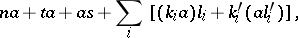where are arbitrary elements of and 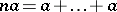( terms, ). If is a ring with a unit element, the term 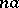may be omitted. In particular, for an algebra over a field,

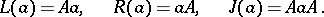In a semi-group 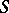one also has left, right and two-sided ideals generated by an element , and they are equal, respectively, to

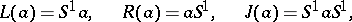where 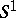is the semi-group coinciding with if 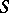contains a unit, and is otherwise obtained from by external adjunction of a unit.

The principal ideal of a lattice 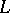generated by an element is identical with the set of all such that 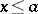; it is usually denoted by 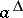, , 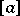or if the lattice has a zero. Thus,

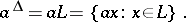In a lattice of finite length all ideals are principal.

Comments

Let be an integral domain with field of fractions . A principal fractional ideal of 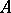is an -submodule of of the form for some .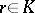

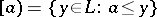Let be a lattice. Dual to the principal ideal generated by one has the principal dual ideal or principal filter determined by , which is the set . The principal ideal in determined by is also denoted (more accurately) by .

A partially ordered set is a complete lattice if and only if it has a zero and every ideal in is principal.

References

[a1]	E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1963) pp. Chapt. IV, Sect. 3 (Translated from Russian)
[a2]	L. Beran, "Orthomodular lattices" , Reidel (1985) pp. 4ff
[a3]	G. Grätzer, "Lattice theory" , Freeman (1971)
[a4]	A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) pp. 78; 86; 162 (Translated from Russian)