Zonal harmonics

zonal harmonic polynomials

Zonal harmic polynomials are spherical harmonic polynomials (cf. also Spherical harmonics) that assume constant values on circles centred on an axis of symmetry. They characterize single-valued harmonic functions on simply-connected domains with rotational symmetry.

To be specific, one introduces the spherical coordinates as , , , where . The zonal harmonics are the polynomial solutions of the Laplace equation

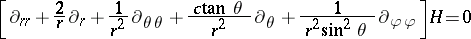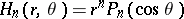that are axially symmetric (i.e. independent of the angle ). They can be expressed in terms of Legendre polynomials of degree , as for 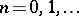, and form a complete orthogonal set of functions in 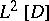, wher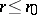e : . The vanish on cones that divide a sphere centred at the origin into zones, hence the name zonal harmonics. The are sometimes referred to as solid zonal harmonics and the 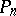as surface zonal harmonics.

Applications.

Two types of applications arise in classical potential theory (see [a4], [a6], [a7]).

In the first, one determines the potential in a sphere from its boundary values 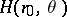. By specifying appropriate regularity conditions, the orthogonality of the Legendre polynomials is used to expand 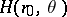as the Fourier–Legendre series . The potential in the sphere is recovered as 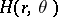. The exterior boundary value problem is formulated by means of the Kelvin transformation 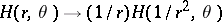. The potential between two concentric spheres is determined by combining solutions of the interior and the exterior problems.

In the second, one determines the potential at points in space from its values on a segment of the symmetry axis. The solution relies on the fact that along this axis the zonal harmonics , 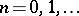. Thus, if 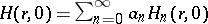, then for , where is the radius of convergence of the Taylor series.

Relation with analytic functions.

There are many connections between the properties of the potentials 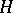and those of analytic functions 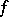of a complex variable (cf. also Analytic function; Harmonic function). One such connection, related to the previous example, concerns singularities and uses the generating function for zonal harmonics to construct reciprocal integral transforms connecting 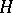with 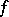. The following fact is immediate (see [a3], [a8]). Let 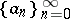be a sequence of real constants for which 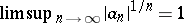. Consider the associated harmonic and analytic functions 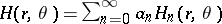and 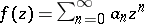, which are regular for 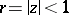. Then the boundary point 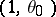is a singularity of 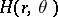if and only if the boundary point 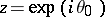is a singularity of . Thus, the singularities of solutions of a singular partial differential equation are characterized in terms of those of associated analytic functions and vice versa.

From the 1950s onwards, an extensive literature has developed using integral transform methods to study solutions of large classes of multi-variable partial differential equations. The analysis is based on the theory of analytic and harmonic functions in several variables. Zonal harmonics play an important role in axially symmetric problems in 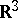(see [a1], [a2], [a3], [a5]).

References

[a1]	H. Begher, R.P. Gilbert, "Transmutations, transformations and kernel functions" , Monographs and Surveys in Pure and Applied Math. , 58–59 , Pitman (1992)
[a2]	S. Bergman, "Integral operators in the theory of linear partial differential equations" , Springer (1963)
[a3]	R.P. Gilbert, "Function theoretic methods in partial differential equations" , Math. in Sci. and Engin. , 54 , Acad. Press (1969)
[a4]	O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929)
[a5]	M. Kracht, E. Kreyszig, "Methods of complex analysis in partial differential equations with applications" , Wiley/Interscience (1988)
[a6]	W.D. MacMillan, "The theory of the potential" , Dover (1958)
[a7]	P.M. Morse, H. Feshbach, "Methods of theoretical physics" , 1–2 , McGraw-Hill (1953)
[a8]	G. Szegö, "On the singularities of real zonal harmonic series" J. Rat. Mech. Anal. , 3 (1954) pp. 561–564