Wiener field
A generalization of the notion of Wiener process for the case of multivariate time. This generalization can be performed in two ways.
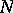 -parameter Wiener field (Brownian motion).
-parameter Wiener field (Brownian motion).
Let 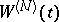 be a Gaussian separable real-valued field on
be a Gaussian separable real-valued field on 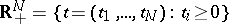 with zero mean and covariance function
with zero mean and covariance function
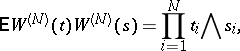 |
where  . Such a field can be regarded as the distribution function of a white noise
. Such a field can be regarded as the distribution function of a white noise 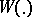 on
on 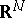 , which is a random function on bounded Borel sets in
, which is a random function on bounded Borel sets in 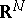 such that
such that 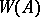 has a normal distribution with zero mean and covariance function
has a normal distribution with zero mean and covariance function 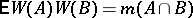 [a11]. Here,
[a11]. Here, 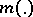 denotes the Lebesgue measure on
denotes the Lebesgue measure on 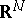 . The following equality holds:
. The following equality holds:  , where
, where 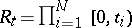 is a parallelepiped in
is a parallelepiped in 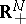 .
.
The random field 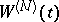 was introduced by T. Kitagava [a14] in connection with its applications to statistical problems. N.N. Chentsov proved the almost sure continuity of the sample functions of
was introduced by T. Kitagava [a14] in connection with its applications to statistical problems. N.N. Chentsov proved the almost sure continuity of the sample functions of 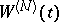 [a3]. For any fixed
[a3]. For any fixed 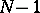 time variables,
time variables, 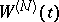 is a one-parameter Wiener process as a function of the free time variable. Some properties of
is a one-parameter Wiener process as a function of the free time variable. Some properties of 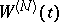 are similar to the corresponding properties of the Wiener process: the sample functions of
are similar to the corresponding properties of the Wiener process: the sample functions of 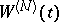 almost surely satisfy Hölder's stochastic condition with exponent
almost surely satisfy Hölder's stochastic condition with exponent 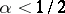 [a2]; various forms of the law of the iterated logarithm hold true ([a5], [a18], [a20]). An exact formula for
[a2]; various forms of the law of the iterated logarithm hold true ([a5], [a18], [a20]). An exact formula for 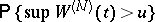 exists only for the Wiener process. For
exists only for the Wiener process. For 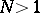 , only lower and upper bounds (
, only lower and upper bounds (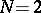 , [a12]) and some asymptotic formulas for
, [a12]) and some asymptotic formulas for 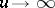 [a21] have been derived so far (1998). The level sets of
[a21] have been derived so far (1998). The level sets of 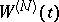 have an extremely complicated geometric and topological structure ([a8], [a9], [a10], [a13]). R.J. Adler [a1] showed that the Hausdorff dimension of these sets equals
have an extremely complicated geometric and topological structure ([a8], [a9], [a10], [a13]). R.J. Adler [a1] showed that the Hausdorff dimension of these sets equals 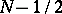 .
.
The Wiener process is a Markov process: conditional of the present value  , the past
, the past 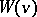 (
(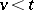 ) and the future
) and the future 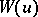 (
(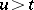 ) are independent. For the multivariate case there are several definitions of the Markovian property. Let
) are independent. For the multivariate case there are several definitions of the Markovian property. Let 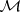 denote a family of Jordan surfaces in
denote a family of Jordan surfaces in 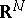 . Each such surface
. Each such surface 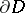 divides
divides 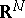 into two parts:
into two parts: 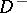 , the interior of
, the interior of 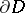 , or the "past" , and
, or the "past" , and 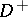 , the exterior of
, the exterior of 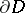 , or the "future" . A random field
, or the "future" . A random field 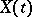 is said to be Markovian with respect to the family
is said to be Markovian with respect to the family 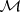 if for arbitrary
if for arbitrary 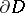 from
from 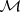 and arbitrary
and arbitrary 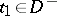 ,
, 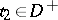 , the random variables
, the random variables 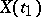 and
and 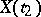 are conditionally independent given
are conditionally independent given 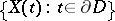 [a24]. A Wiener field
[a24]. A Wiener field  is a Markovian field with respect to the family
is a Markovian field with respect to the family 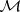 consisting of all finite unions of rectangles whose sides are parallel to the coordinate axes ([a22], [a23]). For
consisting of all finite unions of rectangles whose sides are parallel to the coordinate axes ([a22], [a23]). For 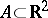 , its sharp field
, its sharp field 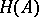 and germ field
and germ field 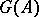 are defined, respectively, by
are defined, respectively, by  and
and  , where
, where 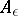 is an
is an  -neighbourhood of
-neighbourhood of 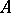 . A Wiener sheet
. A Wiener sheet  is germ Markovian, i.e. for every bounded subset
is germ Markovian, i.e. for every bounded subset 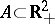 , the fields
, the fields 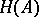 and
and 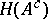 are conditionally independent given
are conditionally independent given 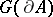 ([a6], [a7], [a22]).
([a6], [a7], [a22]).
Among the objects closely related to 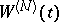 are the Wiener pillow and the Wiener bridge. These are Gaussian random fields (cf. also Random field) on
are the Wiener pillow and the Wiener bridge. These are Gaussian random fields (cf. also Random field) on 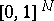 with zero mean and covariance functions
with zero mean and covariance functions
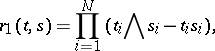 |
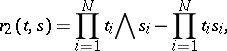 |
respectively.
Lévy 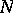 -parameter Brownian motion.
-parameter Brownian motion.
This is a Gaussian random field 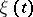 on
on 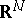 with zero mean and covariance function
with zero mean and covariance function
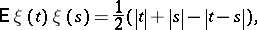 |
where 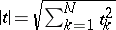 [a15]. When
[a15]. When 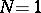 ,
,  becomes a Wiener process. The random variables
becomes a Wiener process. The random variables 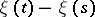 clearly form a Wiener process if
clearly form a Wiener process if 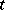 moves along some semi-straight line with terminal point
moves along some semi-straight line with terminal point  .
. 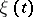 has the following representation in terms of white noise:
has the following representation in terms of white noise:
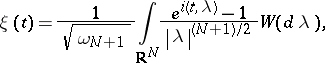 |
where 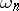 is the surface area of the
is the surface area of the  -dimensional unit sphere [a17]. H.P. McKean Jr. [a16] has shown that
-dimensional unit sphere [a17]. H.P. McKean Jr. [a16] has shown that  is germ Markovian with respect to closed bounded subsets in
is germ Markovian with respect to closed bounded subsets in 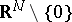 for each odd
for each odd 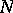 , whereas for each even
, whereas for each even 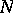 the Markovian property does not hold.
the Markovian property does not hold.
References
| [a1] | R.J. Adler, "The uniform dimension of the level sets of a Brownian sheet" Ann. of Probab. , 6 (1978) pp. 509–518 |
| [a2] | R.J. Adler, "The geometry of random fields" , Wiley (1981) |
| [a3] | N.N. Chentsov, "Wiener random fields depending on several parameters" Dokl. Akad. Nauk SSSR , 106 (1956) pp. 607–609 |
| [a4] | N.N. Chentsov, "A multiparametric Brownian motion Lévy and generalized white noise" Theory Probab. Appl. , 2 (1957) pp. 281–282 |
| [a5] | M. Csőrgő, P. Révész, "Strong approximations in probability and statistics" , Akad. Kiado (1981) |
| [a6] | R.C. Dalang, F. Russo, "A prediction problem for the Brownian sheet" J. Multivariate Anal. , 26 (1988) pp. 16–47 |
| [a7] | R.C. Dalang, J.B. Walsh, "The sharp Markov property of the Brownian sheet and related processes" Acta Math. , 168 (1992) pp. 153–218 |
| [a8] | R.C. Dalang, J.B. Walsh, "Geography of the level sets of the Brownian sheet" Probab. Th. Rel. Fields , 96 (1993) pp. 153–176 |
| [a9] | R.C. Dalang, J.B. Walsh, "The structure of a Brownian bubble" Probab. Th. Rel. Fields , 96 (1993) pp. 475–501 |
| [a10] | R.C. Dalang, T. Mountford, "Nondifferentiability of curves on the Brownian sheet" Ann. of Probab. , 24 (1996) pp. 182–195 |
| [a11] | R.M. Dudley, "Sample functions of the Gaussian process" Ann. of Probab. , 1 (1973) pp. 66–103 |
| [a12] | V. Goodman, "Distribution estimates for functionals of the two-parameter Wiener process" Ann. of Probab. , 4 (1976) pp. 977–982 |
| [a13] | W. Kendall, "Contours of Brownian processes with several-dimensional time" ZWvG , 52 (1980) pp. 269–276 |
| [a14] | T. Kitagava, "Analysis of variance applied to function spaces" Mem. Fac. Sci. Kyushu Univ. Ser. A , 6 (1951) pp. 41–53 |
| [a15] | P. Lévy, "Processes stochastiques et mouvement brownien" , Gauthier-Villars (1948) |
| [a16] | H.P. McKean Jr., "Brownian motion with a several-dimensional time" Theory Probab. Appl. , 8 (1963) pp. 335–354 |
| [a17] | G.M. Molchan, "Some problems for Lévy's Brownian motion" Theory Probab. Appl. , 12 (1967) pp. 682–690 |
| [a18] | S. Orey, W. Pruitt, "Sample functions of the N-parameter Wiener process" Ann. of Probab. , 1 (1973) pp. 138–163 |
| [a19] | S.R. Paranjape, C. Park, "Distribution of the supremum of the two-parameter Yeh–Wiener process on the boundary" J. Appl. Probab. , 10 (1973) pp. 875–880 |
| [a20] | S.R. Paranjape, C. Park, "Laws of iterated logarithm of multiparameter Wiener process" J. Multivariate Anal. , 3 (1973) pp. 132–136 |
| [a21] | V.I. Piterbarg, "Asymptotic methods in the theory of Gaussian processes and fields" , Amer. Math. Soc. (1996) |
| [a22] | Yu.A. Rosanov, "Markov random fields" , Springer (1982) |
| [a23] | J.B. Walsh, "Propagation of singularities in the Brownian sheet" Ann. of Probab. , Ann. 10 (1982) pp. 279–288 |
| [a24] | M.I. Yadrenko, "Spectral theory of random fields" , Optim. Software (1983) |
Wiener field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener_field&oldid=24596