Wodzicki residue

non-commutative residue

In algebraic quantum field theory (cf. also Quantum field theory), in order to write down an action in operator language one needs a functional that replaces integration [a1]. For the Yang–Mills theory (cf. Yang–Mills field) this is the Dixmier trace, which is the unique extension of the usual trace to the ideal of the compact operators such that the partial sums of its spectrum diverge logarithmically as the number of terms in the sum. The Wodzicki (or non-commutative) residue [a3] is the only extension of the Dixmier trace to the class of pseudo-differential operators (DOs; cf. Pseudo-differential operator) which are not in . It is the only trace one can define in the algebra of DOs (up to a multiplicative constant), its definition being: , with the Laplace operator. It satisfies the trace condition: . A very important property is that it can be expressed as an integral (local form):

with the co-sphere bundle on (some authors put a coefficient in front of the integral, this gives the Adler–Manin residue).

If 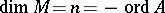( a compact Riemannian manifold, an elliptic operator, ), it coincides with the Dixmier trace, and one has

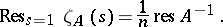The Wodzicki residue continues to make sense for DOs of arbitrary order and, even if the symbols , , are not invariant under coordinate choice, their integral is, and defines a trace. All residues at poles of the zeta-function of a 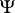DO can be easily obtained from the Wodzicki residue [a2].

References

[a1]	A. Connes, "Noncommutative geometry" , Acad. Press (1994)
[a2]	E. Elizalde, "Complete determination of the singularity structure of zeta functions" J. Phys. , A30 (1997) pp. 2735
[a3]	M. Wodzicki, "Noncommutative residue I" Yu.I. Manin (ed.) , K-Theory, Arithmetic and Geometry , Lecture Notes in Mathematics , 1289 , Springer (1987) pp. 320–399