Finite-dimensional associative algebra
An associative algebra (cf. Associative rings and algebras) 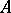 that is also a finite-dimensional vector space over a field
that is also a finite-dimensional vector space over a field 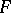 such that
such that
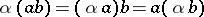 |
for all 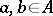 ,
, 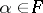 . The dimension
. The dimension  of the space
of the space 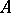 over
over 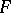 is called the dimension of the algebra
is called the dimension of the algebra 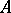 over
over 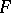 . It is also customary to say that the algebra
. It is also customary to say that the algebra 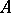 is
is  -dimensional. Every
-dimensional. Every  -dimensional associative algebra
-dimensional associative algebra 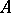 over a field
over a field 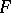 has a faithful representation by matrices of order
has a faithful representation by matrices of order 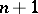 over
over 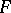 , that is, there is an isomorphism of the algebra
, that is, there is an isomorphism of the algebra 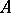 onto a subalgebra of the algebra of all square
onto a subalgebra of the algebra of all square 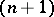 -matrices over
-matrices over 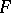 . If
. If 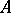 has an identity, then it has a faithful representation by matrices of order
has an identity, then it has a faithful representation by matrices of order  over
over 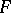 .
.
Let  be a basis of the vector space
be a basis of the vector space 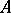 over
over 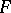 (it is also called a basis of the algebra
(it is also called a basis of the algebra 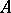 ), and suppose that
), and suppose that
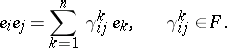 |
The elements 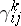 of
of 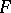 are called the structure constants of the algebra
are called the structure constants of the algebra 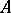 in the given basis. They form a tensor of rank three in the space
in the given basis. They form a tensor of rank three in the space 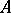 .
.
Main theorems concerning finite-dimensional associative algebras.
The Jacobson radical of a finite-dimensional associative algebra is nilpotent and, if the ground field is separable, it splits off as a semi-direct summand (see Wedderburn–Mal'tsev theorem). A semi-simple finite-dimensional associative algebra over a field splits into a direct sum of matrix algebras over skew-fields. If the ground field 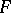 is algebraically closed, then a semi-simple finite-dimensional associative algebra splits into a direct sum of full matrix algebras over
is algebraically closed, then a semi-simple finite-dimensional associative algebra splits into a direct sum of full matrix algebras over 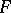 . The simple finite-dimensional algebras are just the full matrix algebras over skew-fields (Wedderburn's theorem). In particular, a finite-dimensional associative algebra without zero divisors is a skew-field. The following are the only finite-dimensional associative algebras with division (that is, skew-fields) over the real field: the real field, the complex field and the skew-field of quaternions (Frobenius' theorem).
. The simple finite-dimensional algebras are just the full matrix algebras over skew-fields (Wedderburn's theorem). In particular, a finite-dimensional associative algebra without zero divisors is a skew-field. The following are the only finite-dimensional associative algebras with division (that is, skew-fields) over the real field: the real field, the complex field and the skew-field of quaternions (Frobenius' theorem).
Many of the structural properties of finite-dimensional associative algebras mentioned here also hold in the larger classes of Noetherian and Artinian rings (see, e.g., Wedderburn–Artin theorem).
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | A.A. Albert, "Structure of algebras" , Amer. Math. Soc. (1939) |
Comments
Skew-fields are also known as division algebras, cf. Division algebra.
The representation theory of finite-dimensional (associative) algebras is a very active branch of mathematics nowadays (1988). Cf., e.g., [a1]–[a2] and Quiver and Representation of an associative algebra.
References
| [a1] | R. Pierce, "Associative algebras" , Springer (1980) |
| [a2] | C.M. Ringel, "Tame algebras and integral quadratic forms" , Lect. notes in math. , 1099 , Springer (1984) |
Finite-dimensional associative algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite-dimensional_associative_algebra&oldid=24069