Bernoulli trials
2020 Mathematics Subject Classification: Primary: 60-01 [MSN][ZBL]
Independent trials, each one of which can have only two results ( "success" or "failure" ) such that the probabilities of the results do not change from one trial to another. Bernoulli trials are one of the principal schemes considered in probability theory.
Let  be the probability of success, let
be the probability of success, let  be the probability of failure, and let 1 denote the occurrence of success, while 0 denotes the occurrence of a failure. The probability of a given sequence of successful or unsuccessful events, e.g.
be the probability of failure, and let 1 denote the occurrence of success, while 0 denotes the occurrence of a failure. The probability of a given sequence of successful or unsuccessful events, e.g.
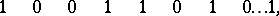 |
is equal to
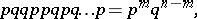 |
where  is the number of successful events in the series of
is the number of successful events in the series of  trials under consideration. Many frequently occurring probability distributions are connected with Bernoulli trials. Let
trials under consideration. Many frequently occurring probability distributions are connected with Bernoulli trials. Let  be the random variable which is equal to the number of successes in
be the random variable which is equal to the number of successes in  Bernoulli trials. The probability of the event
Bernoulli trials. The probability of the event  is then
is then
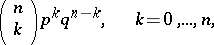 |
i.e.  has a binomial distribution. As
has a binomial distribution. As  , this distribution can be approximated by the normal distribution or by the Poisson distribution. Let
, this distribution can be approximated by the normal distribution or by the Poisson distribution. Let  be the number of trials prior to the first success. The probability of the event
be the number of trials prior to the first success. The probability of the event 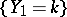 then is
then is
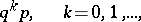 |
i.e. 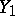 has a geometric distribution. If
has a geometric distribution. If 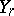 is the number of failures which precede the
is the number of failures which precede the  -th appearance of a successful result,
-th appearance of a successful result,  has the so-called negative binomial distribution. The number of successful outcomes of Bernoulli trials can be represented as the sum
has the so-called negative binomial distribution. The number of successful outcomes of Bernoulli trials can be represented as the sum 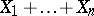 of independent random variables, in which
of independent random variables, in which 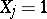 if the
if the 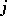 -th trial was a success, and
-th trial was a success, and 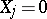 otherwise. This is why many important laws of probability theory dealing with sums of independent variables were originally established for Bernoulli trial schemes (cf. Bernoulli theorem ((weak) Law of large numbers); Strong law of large numbers; Law of the iterated logarithm; Central limit theorem; etc.).
otherwise. This is why many important laws of probability theory dealing with sums of independent variables were originally established for Bernoulli trial schemes (cf. Bernoulli theorem ((weak) Law of large numbers); Strong law of large numbers; Law of the iterated logarithm; Central limit theorem; etc.).
A rigorous study of infinite sequences of Bernoulli trials requires the introduction of a probability measure in the space of infinite sequences of zeros and ones. This may be done directly or by the method illustrated for the case  below. Let
below. Let 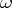 be a number, uniformly distributed on the segment
be a number, uniformly distributed on the segment  , and let
, and let
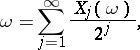 |
where 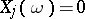 or 1, be the expansion of
or 1, be the expansion of 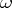 into a binary fraction. Then the
into a binary fraction. Then the  ,
,  are independent and assume the values 0 and 1 with probability
are independent and assume the values 0 and 1 with probability  each, i.e. the succession of zeros and ones in the expansion of
each, i.e. the succession of zeros and ones in the expansion of  is described by the Bernoulli trial scheme with
is described by the Bernoulli trial scheme with 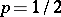 . However, the measure on
. However, the measure on 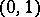 can also be specified so as to obtain Bernoulli trials with any desired
can also be specified so as to obtain Bernoulli trials with any desired 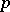 (if
(if 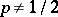 the measure obtained is singular with respect to the Lebesgue measure).
the measure obtained is singular with respect to the Lebesgue measure).
Bernoulli trials are often treated geometrically (cf. Bernoulli random walk). Certain probabilities of a large number of events connected with Bernoulli trials were computed in the initial stage of development of probability theory in the context of the ruin problem.
References
| [1] | B.V. Gnedenko, "The theory of probability" , Chelsea, reprint (1962) (Translated from Russian) MR0149513 Zbl 0102.34402 |
| [2] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1957–1971) MR0779091 MR0779090 MR0270403 MR0228020 MR1534302 MR0243559 MR0242202 MR0210154 MR1570945 MR0088081 MR1528130 MR0067380 MR0038583 Zbl 0598.60003 Zbl 0598.60002 Zbl 0219.60003 Zbl 0155.23101 Zbl 0158.34902 Zbl 0151.22403 Zbl 0138.10207 Zbl 0115.35308 Zbl 0077.12201 Zbl 0039.13201 |
| [3] | M. Kac, "Statistical independence in probability, analysis and number theory" , Math. Assoc. Amer. (1963) MR1530983 MR0110114 Zbl 0112.09101 |
Bernoulli trials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_trials&oldid=24021