Veronese mapping

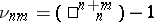A special regular mapping of a projective space; named after G. Veronese. Let be positive integers, , and 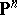, 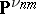projective spaces over an arbitrary field (or over the ring of integers), regarded as schemes; let be projective coordinates in 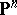, and let 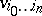, , 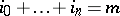be projective coordinates in 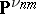. The Veronese mapping is the morphism

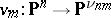given by the formulas 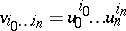, 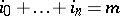. The Veronese mapping may be defined in invariant terms as a regular mapping given by a complete linear system , where 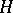is a hyperplane section in 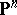. The Veronese mapping is a closed imbedding; its image 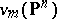is called a Veronese variety, and is defined by the equations

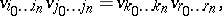where . For instance, 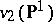is the curve represented by the equatio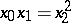n in 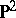. The degree of a Veronese variety is 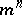. For any hypersurface

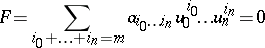in its image with respect to the Veronese mapping 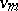is the intersection of the Veronese variety 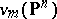with the hyperplane

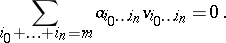Owing to this fact, Veronese mappings may be used to reduce certain problems on hypersurfaces to the case of hyperplane sections.

References

[1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)

Comments

The image of 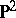in 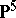under the Veronese imbedding (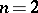, 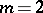) is called the Veronese surface.

References

[a1]	P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 178; 674; 179; 349; 525; 532; 535; 632; 743
[a2]	R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 13; 170; 316; 381