Projective module

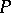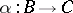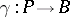A module satisfying any of the following equivalent conditions: 1) for any epimorphism of modules and any homomorphism there is a homomorphism such that 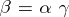; 2) the module 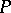is a direct summand of a free module; 3) the functor 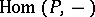is exact (cf. Exact functor); or 4) any epimorphism 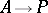of modules splits.

Kaplansky's theorem [2], asserting that every projective module is a direct sum of projective modules with countably many generators, reduces the study of the structure of projective modules to the countable case. Projective modules with finitely many generators are studied in algebraic 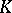-theory. The simplest example of a projective module is a free module. Over rings decomposable into a direct sum there always exist projective modules different from free ones. The coincidence of the class of projective modules and that of free modules has been proved for local rings [2], and for rings of polynomials in several variables over a field (see [3], [4]).

References

[1]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[2]	J. Kaplansky, "Projective modules" Ann. of Math. , 68 : 2 (1958) pp. 372–377
[3]	A.A. Suslin, "Projective modules over a polynomial ring are free" Soviet Math. Dokl. , 17 : 4 (1976) pp. 1160–1164 Dokl. Akad. Nauk SSSR , 229 : 5 (1976) pp. 1063–1066
[4]	D. Quillen, "Projective modules over polynomial rings" Invent. Math. , 36 (1976) pp. 167–171

Comments

The theorem that over a ring 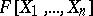of polynomials in several variables over a field every finitely-generated projective module is free is known as the Quillen–Suslin theorem. The question was raised by J.P. Serre in 1955, [a2], and the statement is also still known as Serre's conjecture. For a complete and detailed discussion, cf. [a3].

In [a5], the Quillen–Suslin theorem is formulated as: If 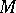is a finitely-generated projective 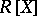-module and 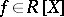is a monic polynomial such that 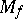is a free 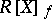-module, then 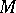is a free 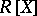-module.

Quillen's proof of the Quillen–Suslin theorem uses Horrock's theorem: Let 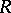be a commutative local ring and 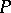a finitely-generated projective module over 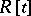. Then if 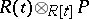is a free 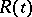-module, 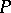is a free -module. A second main ingredient is Quillen's patching theorem. Let be a ring. An -module 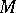is extended (from 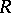) if there exists an 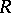-module 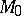such that . The patching theorem now says that if 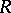is a commutative ring and 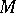is a finitely-presented 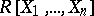-module, then 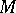is extended from 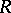if and only if for every maximal ideal 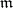of 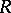the localization 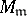is extended from 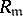. In this terminology one has a generalized Quillen–Suslin theorem: If 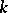is a commutative regular ring of Krull dimension 2, then every finitely-generated projective module over 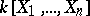is extended from .

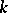The Murthy–Horrock theorem says that every finitely-generated projective module over 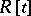is free if 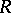is a commutative regular local ring of Krull dimension 2.

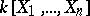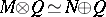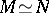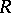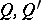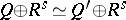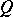The Suslin monic polynomial theorem played a major role in the study of cancellation theorems over . (Cancellation theorems are theorems of the type: If , then . For instance, there is the Bass cancellation theorem, which says that if is a commutative Noetherian ring of Krull dimension and are finitely-generated projective modules which are stably isomorphic, i.e. for some , and the rank of is 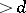, then 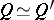.) The monic polynomial theorem says that if 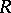is a commutative Noetherian ring of Krull dimension 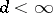and is an ideal in 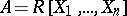of height 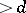, then there exist new variables in 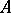such that 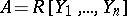and such that contains a polynomial which is monic as a polynomial in . For 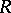a field this essentially becomes the Noether normalization theorem.

A commutative ring 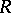is said to be a Hermite ring if every finitely-generated stably free modul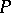e (i.e. 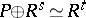for some 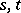) is free.

Serre's conjecture does not necessarily hold for 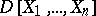if and is a (non-commutation) division ring, [a4]. The quadratic analogue of Serre's conjecture asks whether a finitely-generated projective module over 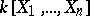equipped with a quadratic, symmetric bilinear, or symplectic form is necessarily extended from a similar object over 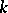. This is not always the case, cf. [a3], Chapt. VI, for more details.

References

[a1]	H. Bass, "Algebraic 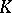-theory" , Benjamin (1968)
[a2]	J.-P. Serre, "Faisceaux algébriques cohérents" Ann. of Math. , 61 (1975) pp. 197–278
[a3]	T.Y. Lam, "Serre's conjecture" , Springer (1978)
[a4]	M. Ojanguran, R. Sridharan, "Cancellation of Azumaya algebras" J. of Algebra , 18 (1971) pp. 501–505
[a5]	E. Kunz, "Introduction to commutative algebra and algebraic geometry" , Birkhäuser (1985)