Canonical curve

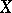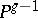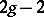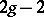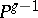The image of an algebraic curve under a canonical imbedding. If a curve is not hyper-elliptic and has genus 2, then its image in the projective space under a canonical imbedding has degree and is a normal curve. Conversely, any normal curve of degree in is a canonical curve for some curve of genus 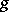. Two algebraic curves (with the above condition) are birationally isomorphic if and only if their canonical curves are projectively equivalent. This reduces the problem of the classification of curves to that of the theory of projective invariants and provides the possibility of constructing a moduli variety of algebraic curves . For small 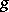it is possible to given an explicit geometric description of canonical curves of genus 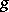. Thus, for genus 4 canonical curves are intersections of quadrics and cubics in 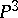, while for genus 5 they are intersections of three quadrics in .

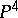References

[1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)
[2a]	J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955)
[2b]	D. Mumford, "Geometric invariant theory" , Springer (1965)
[3]	R.J. Walker, "Algebraic curves" , Springer (1978)
[4]	F. Severi, "Vorlesungen über algebraische Geometrie" , Teubner (1921)

Comments

The degree of a projective algebraic variety 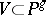of dimension is the number of points of intersection with a generic hyperplane of dimensio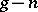n in 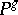. Thus, the degree of a plane curve given by a homogeneous equatio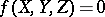n in 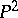is equal to the degree of the polynomial 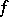. See Algebraic curve for the definition of genus, and other notations occurring above.

References

[a1]	E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1984)
[a2]	D. Mumford, "Curves and their Jacobians" , Univ. Michigan Press (1976)