Adams conjecture

In [a1], J.F. Adams was studying the order of the image of the -homomorphism and related topics. He was led to the following conjecture: Let be a real vector bundle over a finite CW-complex , let be an integer and let be the Adams operation (cf. Cohomology operation). Then for some , is fibre homotopy trivial. In [a4], D.G. Quillen proposed an approach to this conjecture which used some ideas from algebraic geometry and, in particular, étale homotopy theory. This approach was completed by E. Friedlander [a3]. In [a5], Quillen solved the conjecture by a different approach. This approach lead to important results in algebraic -theory and lead to Quillen's definition of higher algebraic -groups. Another proof was discovered by J. Becker and D. Gottlieb [a2]. Their proof uses only techniques from algebraic topology and so could be considered elementary. They introduced the transfer into fibre bundle theory (cf. also Becker–Gottlieb transfer). Previously, transfers required that the fibre be discrete. This work, too, has had a lot of influence. The Adams conjecture has generated a lot of very interesting mathematics.

References

[a1]	J.F. Adams, "On the groups 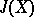. I" Topology , 2 (1963) pp. 181–195
[a2]	J. Becker, D. Gottlieb, "The transfer map and fiber bundles" Topology , 14 (1975) pp. 1–12
[a3]	E. Friedlander, "Fibrations in etale homotopy theory" IHES Publ. Math. , 42 (1972)
[a4]	D.G. Quillen, "Some remarks on etale homotopy theory and a conjecture of Adams" Topology , 7 (1968) pp. 111–116
[a5]	D.G. Quillen, "The Adams conjecture" Topology , 10 (1971) pp. 67–80